Test case of Magnetostatic

1. Introduction

In this page, I present the test case of Maxwell Quasi Static Problem in A-V Formulation with gauge condition for a geometry of torus surrounded by air for stationnary case in Axisymmetrical case.

2. Run the calculation

The command line to run this case is :

    mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=magnetostatic.cfg --cfpdes.gmsh.hsize=1e-3

3. Data Files

The case data files are available in Github here :

4. Equation

We solve A-V Formulation in axisymmetric (MagStat Axis) in stationary case and we assume that \(V\) is known.

A-V Formulation in axisymmetric coordinates in Stationary Case
\[\text{(Magstat Axis)} \left\{ \begin{matrix} \frac{1}{\mu} \Delta \Phi + \frac{2}{\mu \, r} \frac{\partial \Phi}{\partial r} + \sigma \frac{\partial V}{\partial \theta} = 0 & \text{on } \Omega^{axis} & \text{(MagStat-1 Axis)} \\ V = \frac{U}{2\pi} \, \theta & \text{ on } \Omega_c^{axis} \\ A_{\theta} = 0 & \text{ on } \Gamma_D^{axis} & \text{(D Axis)} \\ \frac{\partial A_{\theta}}{\partial \mathbf{n}^{axis}} = 0 & \text{ on } \Gamma_N^{axis} & \text{(N Axis)} \end{matrix} \right.\]

With :

  • \(\Phi = r A_{\theta}\) : \(A_{\theta}\) component \(\theta\) of potential magnetic field

  • \(\sigma\) : electric conductivity \(S/m\)

  • \(\mu\) : electric permeability \(kg/A^2/S^2\)

  • \(U\) : tension \(Volt\)

5. Geometry

The geometry is a torus of a conductor in cartesian coordinates \((x,y,z)\) or rectangle in axisymmetric coordinates \((r,z)\), surrounded by air.

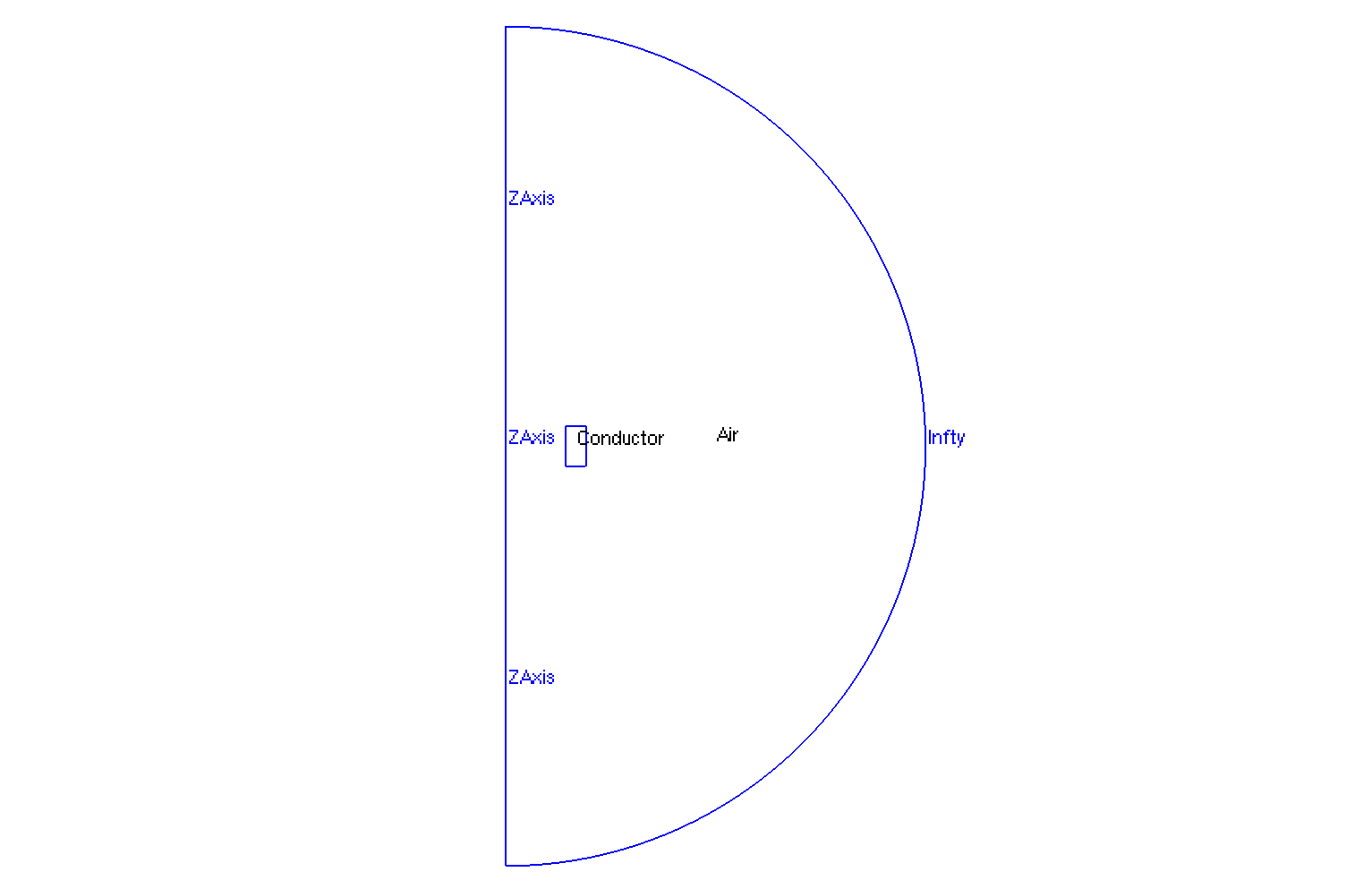
1torus axis
Geometry in Axisymmetrical cut
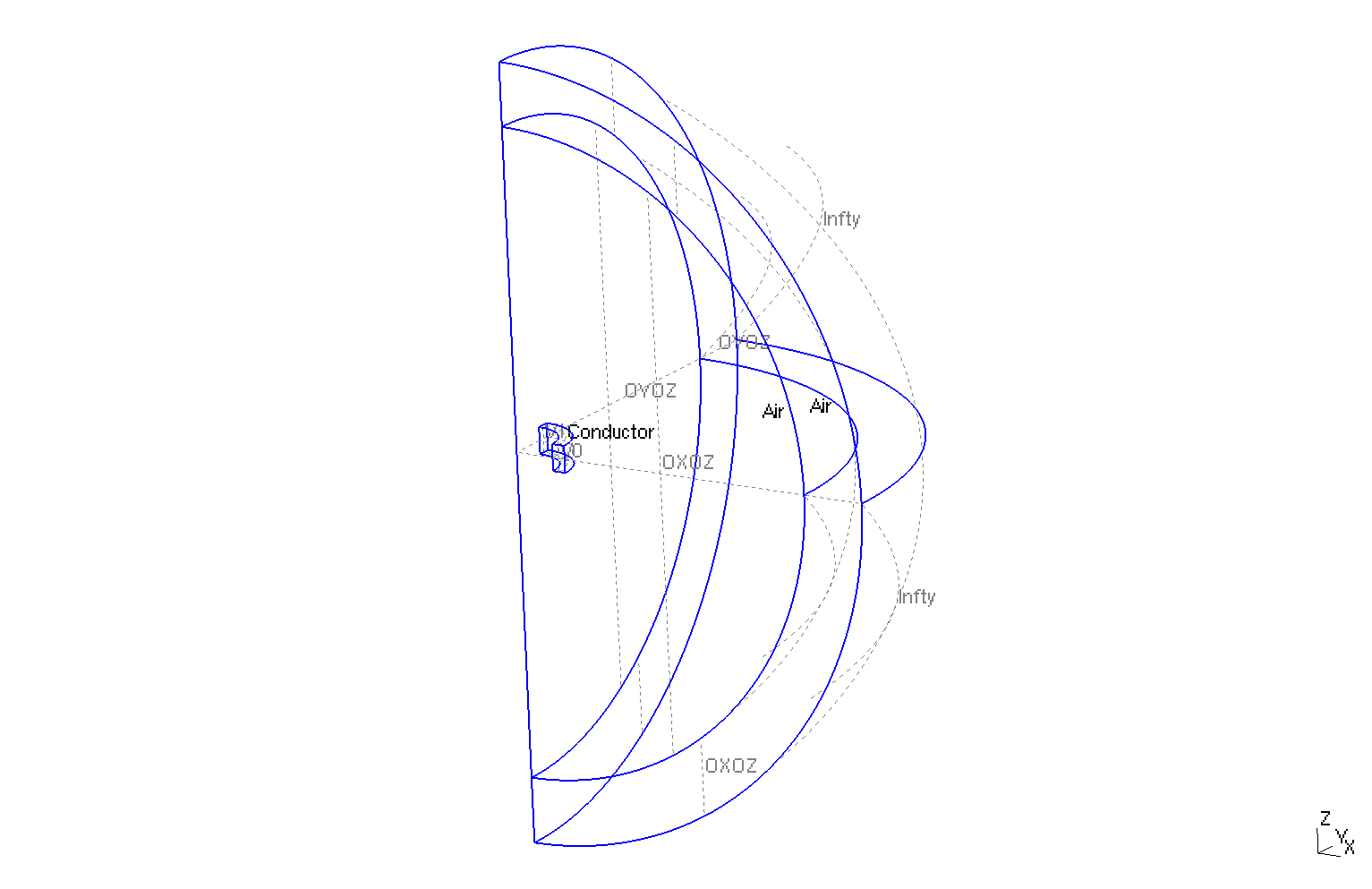
1torus 3d
Geometry in three dimensions

The geometrical domains are :

  • Conductor : the torus, composed by conductor material

  • Air : the air surround Conductor

    • zAxis : a bound of Air, correspond to \(Oz\) axis (\(\{(z,r), \, z=0 \}\))

    • infty : the rest of bound of Air

Symbol

Description

value

unit

\(r_{int}\)

interior radius of torus

\(75e-3\)

m

\(r_{ext}\)

exterior radius of torus

\(100.2e-3\)

m

\(z_1\)

half-height of torus

\(25e-3\)

m

\(r_{infty}\)

radius of infty border

\(5*r_{ext}\)

m

6. Boundary Conditions

We impose the Dirichlet boundary conditions :

  • On zAxis : \(\Phi = 0\) (\(A_{\theta} = 0\) by symetric argument)

  • On infty : \(\Phi = 0\) (\(A_{\theta} = 0\) we consider the bound of resolution like infty for magnetic field)

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file
    "BoundaryConditions":
    {
        "magnetic":
        {
            "Dirichlet":
            {
                "ZAxis":
                {
                    "expr":"0"
                },
                "Infty":
                {
                    "expr":"0"
                }
            }
        }
    }

7. Weak Formulation

We obtain :

Weak Formulation
\[\scriptsize{ \int_{\Omega^{axis}}{ \frac{1}{\mu} \tilde{\nabla} \Phi \cdot \tilde{\nabla} \phi \ r \ drdz } + \int_{\Omega^{axis}}{\frac{2}{\mu \, r} \frac{\partial \Phi}{\partial r} \, \phi \ r \ drdz} = - \int_{\Omega_c^{axis}}{ \sigma \frac{\partial V}{\partial \theta} \phi \ r \ drdz } }\]

With \(\tilde{\nabla} = \begin{pmatrix} \frac{\partial}{\partial r} \\ \frac{\partial}{\partial z} \end{pmatrix}\)

8. Parameters

The parameters of problem are :

  • On Conductor :

Symbol

Description

Value

Unit

\(V\)

scalar electrical potential

\( U \, \frac{\theta}{2\pi}\)

\(Volt\)

\(U\)

electrical potential

\(1\)

\(Volt / rad\)

\(\sigma\)

electrical conductivity

\(58e6\)

\(S/m\)

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

  • On Air :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

On JSON file, the parameters are writed :

Parameters on JSON file
    "Parameters":
    {
	    "U":"1" // Volt
    }

9. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficient associate to Weak Formulation are :

  • On Conductor :

Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\frac{r}{\mu}\)

\(\beta\)

convection coefficient

\(\begin{pmatrix} \frac{2}{\mu} \\ 0 \end{pmatrix}\)

\(f\)

source term

\(- \sigma \frac{U}{2\pi} \, r\)

  • On Air :

Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\frac{r}{\mu}\)

\(\beta\)

convection coefficient

\(\begin{pmatrix} \frac{2}{\mu} \\ 0 \end{pmatrix}\)

On JSON file, the coefficients are writed :

CFPDEs coefficients on JSON file
    "Materials":
    {
        "Conductor":
        {
            "sigma":58e6,       // S.m-1
            "mu":"4*pi*1e-7",   // kg.m/A2/s2
            "magnetic_c":"x/mu:x:mu",
            "magnetic_beta":"{2/mu,0}:mu",
            "magnetic_f":"-sigma*U/2/pi*x:sigma:U:x"
        },
        "Air":
        {
            "mu":"4*pi*1e-7",   // kg.m/A2/s2
            "magnetic_c":"x/mu:x:mu",
            "magnetic_beta":"{2/mu,0}:mu"
        }
    }

10. Numeric Parameters

  • Mesh size :

    • Interior of torus : \(0.001 m\)

    • Far of torus : \(0.004 m\)

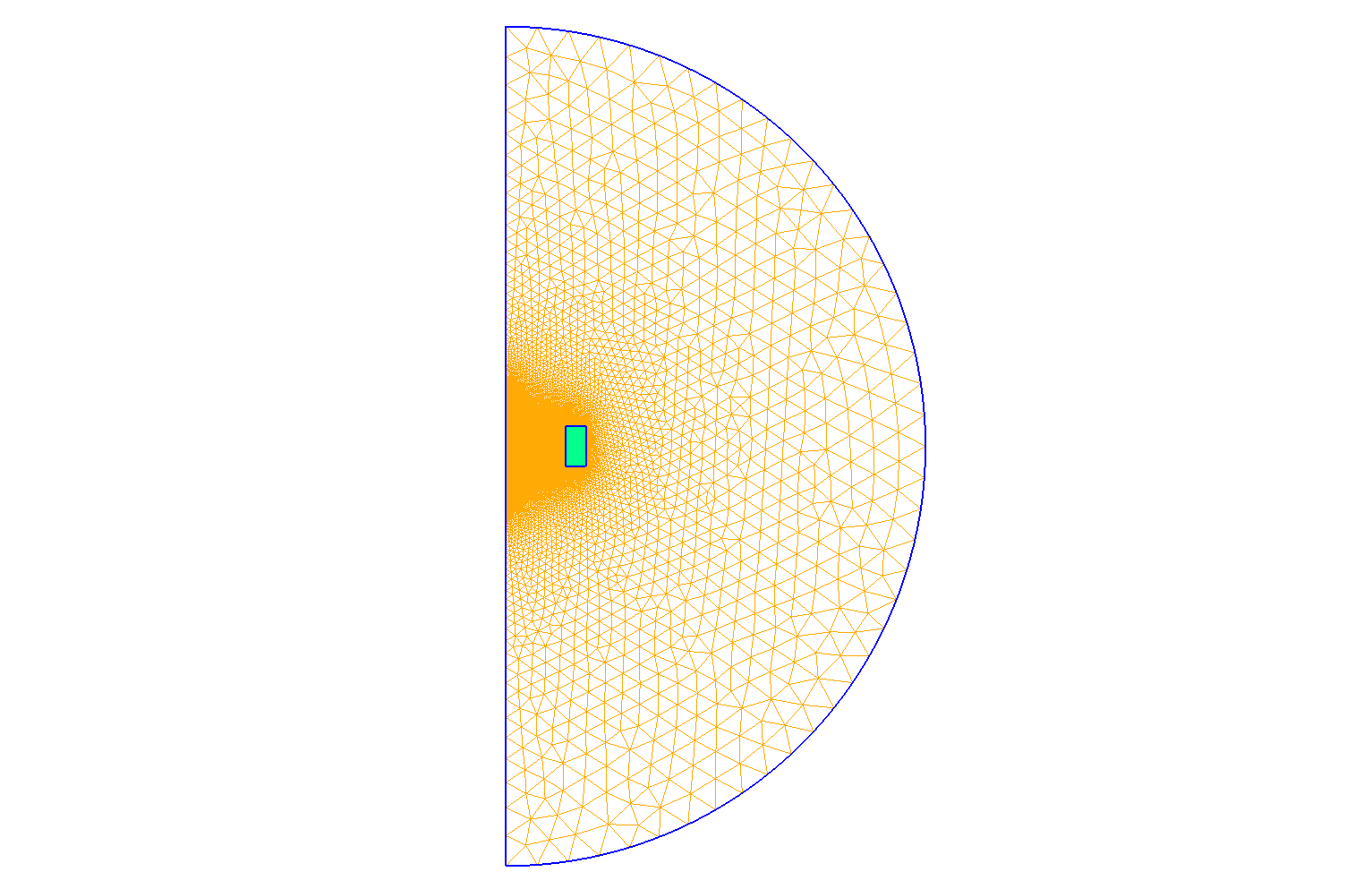
1torus axis mesh
Mesh of Geometry

11. Result

The analytical solve of potential magnetic field and magnetic field (the cyan curve on plots) is computed by python3’s module MagnetTools.MagnetTools. The module based on paper : spire. The python3’s script : Edit the file.

11.1. Magnetic Potential Field

The magnetic potential field \(\mathbf{A}\) is writed :

\[ \mathbf{B} = \nabla \times \mathbf{A}\]
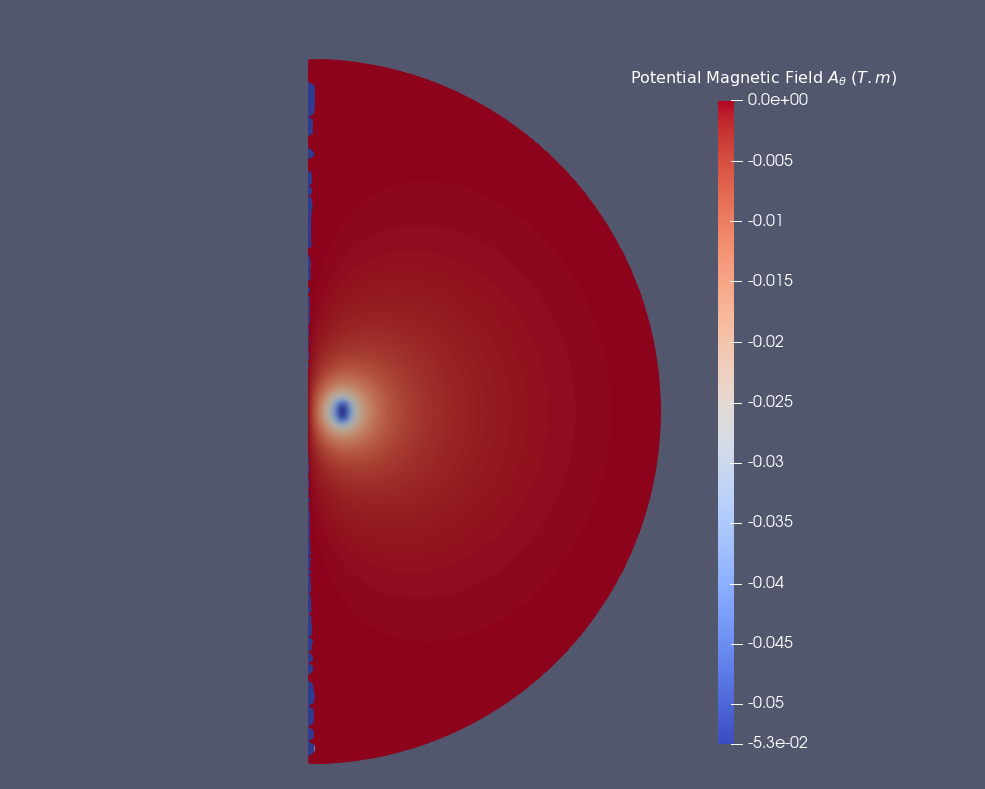
screenshot Ath
\(A_{\theta} (A.m)\) on Or axis

I plot the magnetic potential field \(A_{\theta}\) on \(O_r\) axis solve with P1 and P2 elements with analytical solve (computed with python3’s script).

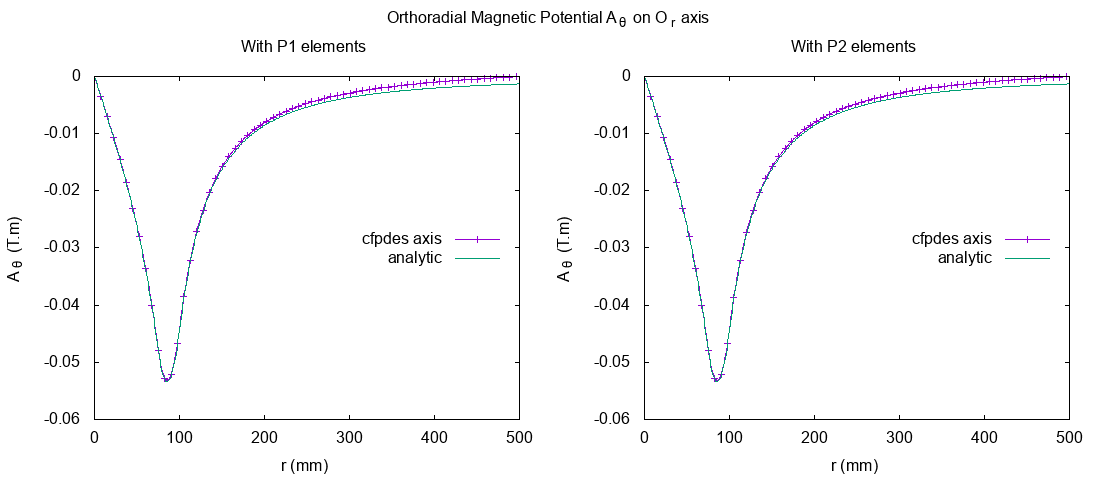
a th Or
\(A_{\theta} (A.m)\) on Or axis

We have a peak near of Conductor, thus the magnetic field \(\mathbf{B}\) rotates around this peak.

11.2. Magnetic Field

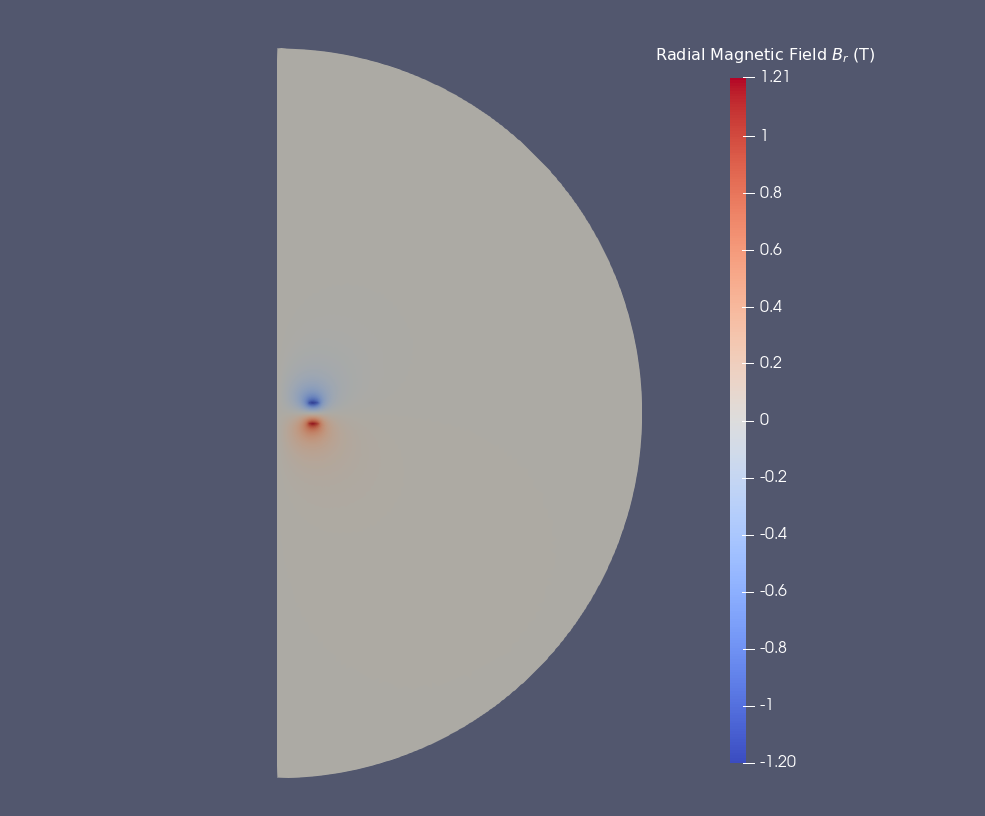
screenshot Br
\(B_r (T)\) on Or axis
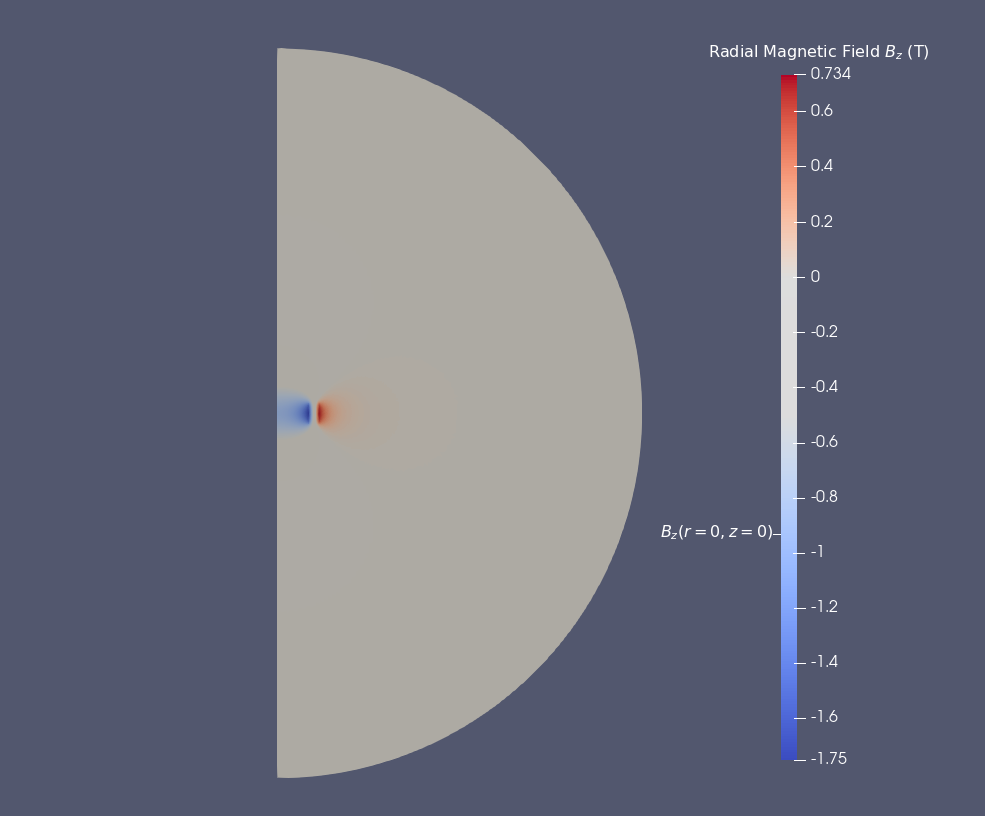
screenshot Bz
\(B_z (T)\) on Or axis

I plot the magnetic field \(A_{\theta}\) on \(O_r\) axis with analytical solve (computed with python3’s script).

Br Or
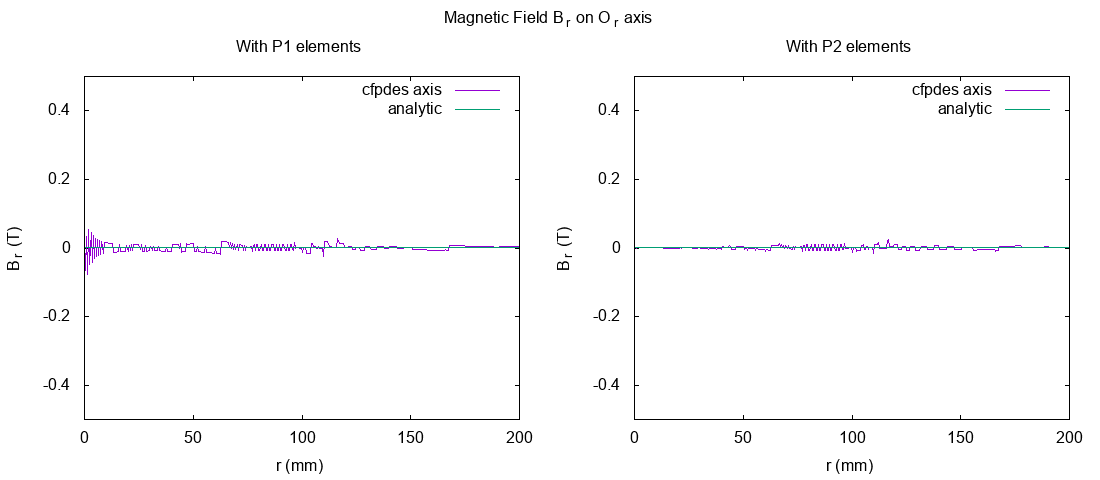
\(B_r (T)\) on Or axis
Bz Or
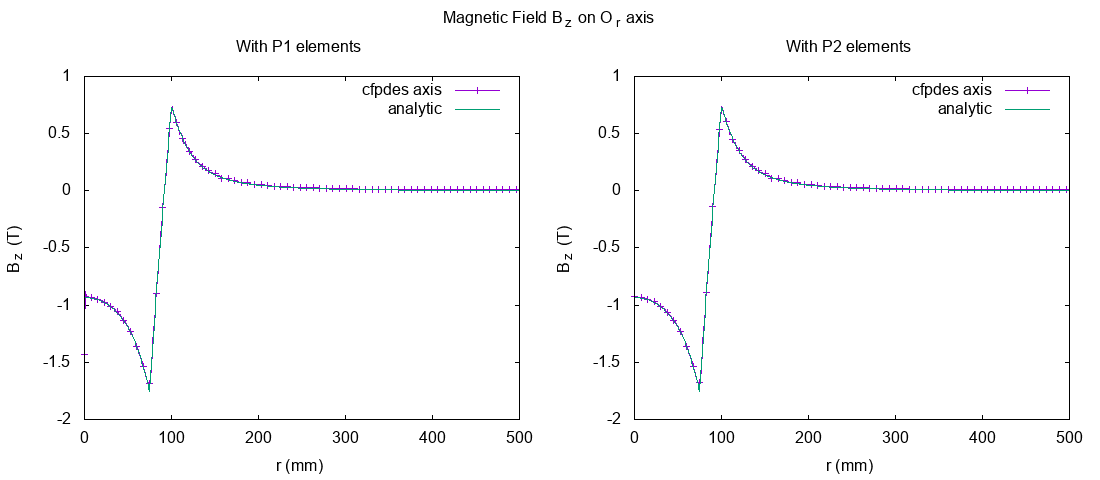
\(B_z (T)\) on Or axis

Around the Or axis, the direction of Magnetic field \(B\) is horizontal, in particulary at \(P0=(r=0,z=0)\).

We can observe a great difference between the resolution with P1 and P2 elements at \(r=0\) :

Bz Or(1)
\(B_z (T)\) on Or axis

The result in P1 elements have instability near of \(r=0\) but not with \(P2\). This instability can be explain by the method of export of Magnetic Field : to have \(B_z\), we export \(\frac{1}{r} \frac{\partial \Phi}{\partial r}\) and the division \(\frac{1}{r}\) near of \(r=0\) can be a problem.

12. References

  • Calcul du champ magnétique pour les géométries axisymétriques simples, Christophe Trophime, 2002, unpublished, Download the PDF