Test case of Thermo-Magnetism with Non-Linear Coefficients in Axisymmetrical case
1. Introduction
In previous page (Test Case in Three Dimensions with Linear Coefficients and Test Case in Axisymmetry with Linear Coefficients), I present the resolution of thermo-magnetism problem with Linear Coefficients (electrical and thermal conductivity are constants). But in reality it isn’t the case, the coefficients depend of temperature.
This page presents the simulation of electromagnetism equation (A-V Formulation) coupled with heat equation with non-linear coefficients on geometry of torus in transient case and axisymmetrical case.
2. Run the calculation
The command line to run this case is :
mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=non-linear.cfg --cfpdes.gmsh.hsize=1e-4
To run the case with adaptative time-step :
sh feelpp_adaptative.sh
3. Data Files
The case data files are available in Github here :
-
CFG file - Edit the file
-
JSON file - Edit the file
-
GEO file - Edit the file
-
SH script for adaptative time-step - Edit the file
4. Equation
In this subsection, we retake the coupled equation (AV+Heat Axis) of Heat equation and AV-Formulation in axisymetrical coordinates with new coefficients.
The domain of resolution of electromagnetism part is \(\Omega^{axis}\) with bounds \(\Gamma^{axis}\), \(\Gamma_D^{axis}\) the bound of Dirichlet conditions and \(\Gamma_N^{axis}\) the bound of Neumann conditions such that \(\Gamma^{axis} = \Gamma_N^{axis} \cup \Gamma_D^{axis}\).
The domain of resolution of heat part is \(\Omega_c^{axis} \subset \Omega^{axis}\) (and the domain of definition of electrical potential \(V\) and electrical conductivity \(\sigma\)) with bounds \(\Gamma_c^{axis}\), \(\Gamma_{Dc}^{axis}\) the bound of Dirichlet conditions and \(\Gamma_{Nc}^{axis}\) the bound of Neumann conditions such that \(\Gamma_c^{axis} = \Gamma_{Nc}^{axis} \cup \Gamma_{Dc}^{axis}\).
Moreover, the electrical conductivity and thermal conductivity for metal can exprim with emprical law :
The resistivity \(\rho\) increase linearly with the temperature such that :
With \(\rho_0\) the resistivity at reference temperature \(T_0\) and \(\alpha\) the temperature coefficient obtained empirically.
Thus the electrical condutivity becomes :
With \(\sigma_0 = \frac{1}{\rho_0}\) the electrical conductivity at reference temperature \(T_0\).
Moreover, the thermal conductivity of metal is proportionnal to its electrical conductivity and its temperature, it’s the Wiedemann-Franz law :
With \(L\) the constant of Lorentz number and is proper of materials.
But, we can rewrite this law :
With thermal conductivity \(k_0\) at reference temperature.
With :
-
\(\Phi = r \, A_{\theta}\), with magnetic potential field \(\mathbf{A} = \begin{pmatrix} A_r \\ A_{\theta} \\ A_z \end{pmatrix}_{cyl}\) such that the magnetic field is writed \(\mathbf{B} = \nabla \times \mathbf{A}\)
-
\(T\) : temperature \((K)\)
-
\(\sigma = \frac{\sigma_0}{1 + \alpha \, \left( T - T_0 \right)}\) : electric conductivity \((S/m)\)
-
\(\sigma_0\) electrical conductivity at reference temperature \(T_0\)
-
\(\alpha\) temperature coefficient
-
-
\(\mu\) : electric permeability \((kg/A^2/S^2)\)
-
\(\rho\) : density \((kg/m^3)\)
-
\(C_p\) : thermal capacity \((J/K/kg)\)
-
\(k = \frac{k}{1 + \alpha \, \left( T - T_0 \right)} \, \frac{T}{T_0}\) : thermal conductivity \((W/m/K)\)
-
\(k_0\) thermal conductivity at reference temperature \(T_0\)
-
\(\alpha\) temperature coefficient
-
-
\(U\) : tension \(Volt\)
| The equation become coupled in both senses, the first equation (AV-1 Axis) depends of temperature \(T\) and the second equation (Heat Axis) depends on \(A_{\theta}\). |
5. Geometry
The geometry is a torus of the conductor in cartesian coordinates \((x,y,z)\) or rectangle in axisymmetric coordinates \((r,z)\), surrounded by air.
.png)
Geometry in axisymmetrical cut
|
.png)
Geometry in axisymmetrical cut loop on Conductor
|
.png)
Geometry in three dimensions
|
.png)
Geometry in three dimensions loop on Conductor
|
The geometrical domains are :
-
Conductor: the torus is composed by conductor material-
Interior: interior surface of conductor ring -
Exterior: exterior surface of conductor ring -
Upper: upper of conductor ring -
Bottom: bottom of conductor ring
-
-
Air: the air surroundConductor-
zAxis: a bound ofAir, correspond to \(Oz\) axis (\(\{(z,r), \, z=0 \}\)) -
infty: the rest of bound ofAir
-
Symbol |
Description |
value |
unit |
\(r_{int}\) |
interior radius of torus |
\(75e-3\) |
m |
\(r_{ext}\) |
exterior radius of torus |
\(100.2e-3\) |
m |
\(z_1\) |
half-height of torus |
\(25e-3\) |
m |
6. Initial/Boundary Conditions
We impose the boundary conditions :
-
Dirichlet :
-
On
zAxis: \(\Phi = 0\) (\(A_{\theta} = 0\) by symetric argument) -
On
infty: \(\Phi = 0\) (\(A_{\theta} = 0\) we consider the bound of resolution like infty for magnetic field)
-
-
Neumann : \(\frac{\partial T}{\partial \mathbf{n}} = 0\) on
InteriorandExterior -
Robin : \(-k \, \frac{\partial T}{\partial \mathbf{n}} = h \, \left( T - T_c \right)\) on
UpperandBottom
We initialize :
-
On
Conductor\(\Phi(t=0,r,z) = 0\) (\(A_{\theta}(t=0,r,z) = 0\)) and \(T(t=0,r,z) = T_i\) -
On
Air\(\Phi(t=0,r,z) = 0\) (\(A_{\theta}(t=0,r,z) = 0\))
On JSON file, the boundary conditions are writed :
"BoundaryConditions":
{
"magnetic":
{
"Dirichlet":
{
"magdir":
{
"markers":["ZAxis","Infty"],
"expr":"0"
}
}
},
"heat":
{
"Robin":
{
"heatrobin":
{
"markers":["Interior","Exterior"],
"expr1":"h*x:h:x",
"expr2":"h*T_c*x:h:T_c:x"
}
}
}
}
On JSON file, the initial conditions are writed :
"InitialConditions":
{
"temperature":
{
"Expression":
{
"Conductor":
{
"expr":"T_i:T_i"
}
}
}
}
7. Weak Formulation
We obtain :
With \(\tilde{\nabla} = \begin{pmatrix} \frac{\partial}{\partial r} \\ \frac{\partial}{\partial z} \end{pmatrix}\)
8. Parameters
The parameters of problem are :
-
On
Conductor:
Symbol |
Description |
Value |
Unit |
\(V\) |
scalar electrical potential |
\( U \, \frac{\theta}{2\pi}\) |
\(Volt\) |
\(U\) |
electrical potential |
\(\left\{ \begin{matrix} t \text{ on } 0s \leq t \leq 1s \\ 1 \text{ on } 1s \leq t \leq 20s \\ 0 \text{ on } 20s \leq t \leq 22s \end{matrix} \right.\) |
\(Volt\) |
\(\sigma\) |
electrical conductivity |
\(\frac{\sigma}{1+\alpha \, \left( 1 + \alpha \, \left( T - T_0 \right) \right)}\) |
\(S/m\) |
\(\sigma_0\) |
electrical conductivity at \(T=T_0\) |
\(58e6\) |
\(S/m\) |
\(\alpha\) |
coefficient ?? |
\(3.6e-3\) |
dimensionless |
\(\mu=\mu_0\) |
magnetic permeability of vacuum |
\(4\pi.10^{-7}\) |
\(kg \, m / A^2 / S^2\) |
\(k\) |
thermal conductivity |
\(\frac{k_0}{1+\alpha \, \left( T-T_0 \right)} \, \frac{T}{T_0}\) |
\(W/m/K\) |
\(k_0\) |
thermal conductivity at \(T=T_0\) |
\(380\) |
\(W/m/K\) |
\(C_p\) |
thermal capacity |
\(380\) |
\(J/K/kg\) |
\(\rho\) |
density |
\(10000\) |
\(kg/m^3\) |
\(h\) |
convective coefficient |
\(80000\) |
\(W/m^2/K\) |
\(T_c\) |
cooling temperature |
\(293\) |
\(K\) |
\(T_i\) |
initial temperature |
\(293\) |
\(K\) |
\(T_0\) |
temperature |
\(293\) |
\(K\) |
-
On
Air:
Symbol |
Description |
Value |
Unit |
\(\mu=\mu_0\) |
magnetic permeability of vacuum |
\(4\pi.10^{-7}\) |
\(kg \, m / A^2 / S^2\) |
On JSON file, the parameters are writed :
"Parameters":
{
"U":"t/1.*(t<1.)+(t>1.)*(t<5.5):t",
"h":80000, // W*m-2*K-1
"T_c":293, // K
"T_i":293 // K
}
9. Coefficient Form PDEs
We use the application Coefficient Form PDEs. The coefficient associate to Weak Formulation are :
-
For MQS equation (Weak MQS Axis) :
-
On
Conductor:
Coefficient
Description
Expression
\(d\)
damping or mass coefficient
\(\sigma = \frac{\sigma}{1+\alpha \, \left( 1 + \alpha \, \left( T - T_0 \right) \right)}\)
\(c\)
diffusion coefficient
\(\frac{r}{\mu}\)
\(\beta\)
convection coefficient
\(\begin{pmatrix} \frac{2}{\mu} \\ 0 \end{pmatrix}\)
\(f\)
source term
\(- \sigma \frac{U}{2\pi} \, r\)
-
On
Air:
Coefficient
Description
Expression
\(c\)
diffusion coefficient
\(\frac{r}{\mu}\)
-
-
For heat equation (Weak Heat Axis), on
Conductor(the temperature isn’t computed onAir) :Coefficient
Description
Expression
\(d\)
damping or mass coefficient
\(\rho \, C_p\)
\(c\)
diffusion coefficient
\(k = \frac{k_0}{1+\alpha \, \left( T-T_0 \right)} \, \frac{T}{T_0}\)
\(f\)
source term
\(\sigma \left( \frac{U}{2\pi} \right)^2 \frac{1}{r}\)
On JSON file, the coeficients are writed :
"Materials":
{
"Conductor":
{
"T0":293,
"alpha":3.6e-3,
"sigma0":58e+6, // S.m-1
"sigma":"sigma0/(1+alpha*(heat_T-T0)):sigma0:alpha:heat_T:T0",
"mu":"4*pi*1e-7", // kg.m/A2/S2
"magnetic_c":"x/mu:x:mu",
"magnetic_beta":"{2/mu,0}:mu",
"magnetic_f":"-sigma*U/2/pi*x:sigma:U:x",
"magnetic_d":"sigma*x:x:sigma",
"k0":380, // W/m/K
"k":"k0/(1+alpha*(heat_T-T0))*heat_T/T0:k0:alpha:heat_T:T0",
"rho":10000, // kg/m3
"Cp":380, // J/K/kg
"heat_c":"k*x:k:x",
"heat_f":"sigma*(U/(2*pi)+magnetic_dphi_dt)*(U/(2*pi)+magnetic_dphi_dt)/x:sigma:U:magnetic_dphi_dt:x",
"heat_d":"rho*Cp*x:rho:Cp:x"
},
"Air":
{
"physics":"magnetic",
"mu":"4*pi*1e-7", // kg.m/A2/s2
"magnetic_c":"x/mu:x:mu",
"magnetic_beta":"{2/mu,0}:mu"
}
}
10. Numeric Parameters
This section show the parameters used to compute the simulation.
-
Size of mesh : \(1 \, mm\)
-
Time Parameters :
-
Time step : I use adaptative time step. Near of brutal changement of current, the time step is little, in other case, the time step is big. I put adaptative time step to have good precision near of changement (cut of current at \(t=22s\)) and to not explose the time of compute. The shell script feelpp_adaptative.sh implements that.
\(\Delta_t = \left\{ \begin{matrix} 0.1s \, \text{for} \, 0s<t<0.9s \\ 0.008s \, \text{for} \, 0.9s<t<1.1s \\ 0.1s \, \text{for} \, 1.1s<t<19.9s \\ 0.008s \, \text{for} \, 19.9s<t<20.1s \\ 0.1 \, \text{for} \, 20.1s<t<22s \end{matrix} \right.\)
-
Initial Time : \(0 \, s\)
-
Final Time : \(22 \, s\)
-
-
Element type : \(P2\) for magnetic equation (\(\mathbf{A}\) and \(P1\) heat equation (\(T\))
Mesh of Geometry
|
11. Result
The analytical solve of potential magnetic field and magnetic field (the cyan curve on plots) is computed by python3’s module MagnetTools.MagnetTools. The module based on paper : spire.
The analytical solve of intensity (and magnetic field) is computed on python3’s script Edit the file.
11.1. Intensity
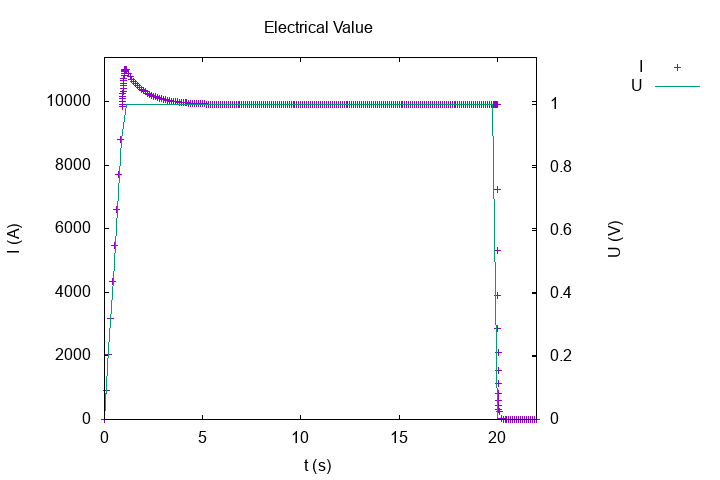
Feelpp compute in post-process, the intensity of circuit :
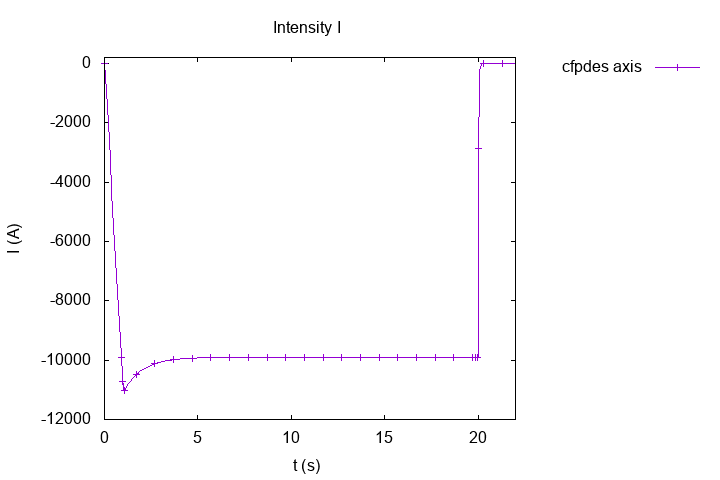
Intensity of current \(I(A)\)
|
We can observe, the intensity form a peak around the first cut (betwenn ramp and tray) and the intensity stabilizes around the value \(I = 113.7 \, kA\), it is the stationnary value give by Ohm Law : \(U = R \, I\) with \(R_{non \, linear} = 14.05 \, picoOhm\).
We can explain this phenomena with plot of intensity and resistance :
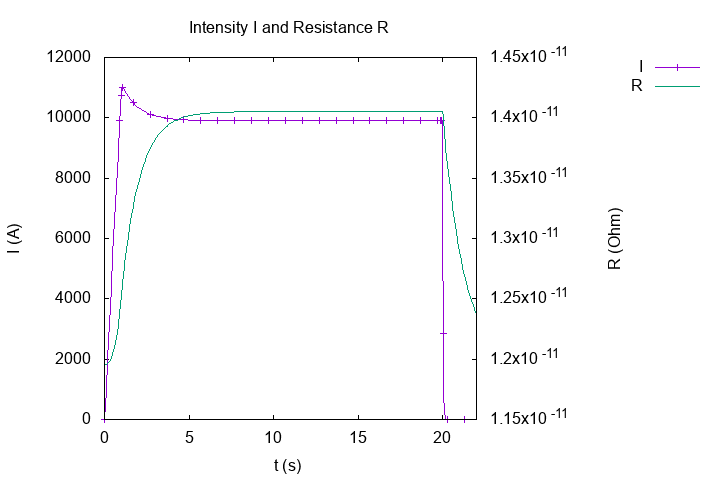
Intensity of current \(I(A)\) and Resistance \(R(Ohm)\)
|
The resistance increases in time because the temperature increases. In begining, the resistance is small, the intensity can have great value but after the resistance increases and the intensity by Ohm law \(U = R \, I\) (recall \(U\) is constant) decreases and stabilzes with the resistance.
11.2. Magnetic field \(B_z\)
Recall, with axisymmetric condition :
Thus \(B_z = \frac{1}{r} \frac{\partial \Phi}{\partial r} \).
-
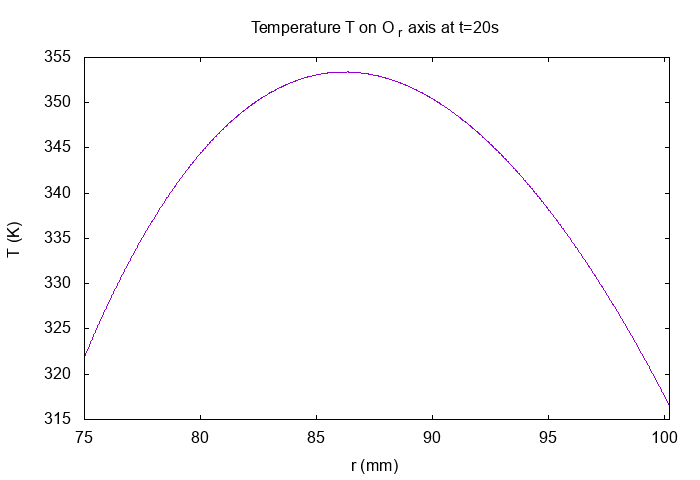
On \(Or\) axis at \(t=20s\)
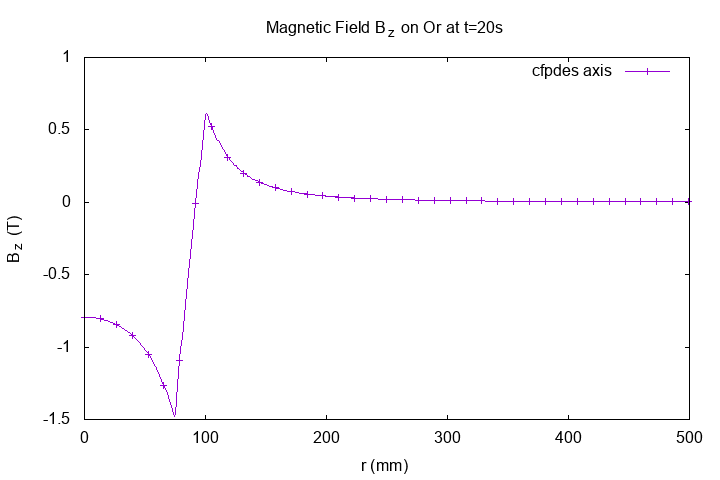
Horizontal Magnetic Field \(B_z(T)\) on Or
|
-
On origin \((0,0,0)\) across the time
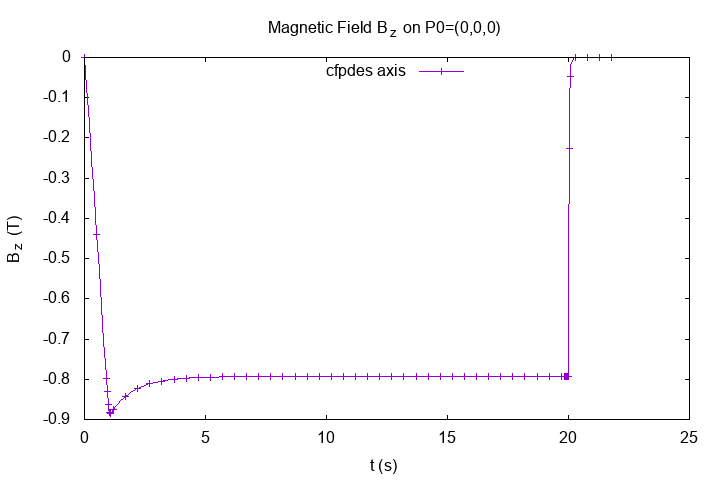
"Horizontal Magnetic Field \(B_z(T)\)
|
-
Magnetic Field across the time :
Horizontal Magnetic Field \(B_z (T)\)
|
12. Comparison with Linear case
I run the simulation of thermo-magnetism problem with Linear coefficients, \(\sigma\) and \(k\) are constants :
-
\(\sigma = \sigma_0\)
-
\(k = k_0\)
If we overlap the result of Non-Linear and Linear, we have :
12.1. Magnetic Field \(\mathbf{B}\)
.png)
Magnetic Field \(\mathbf{B} (T)\) on Or axis
|
.png)
Magnetic Field \(\mathbf{B}(0,0,0) (T)\)
|
We can see, the magnetic field of non-linear simulation is less than the magnetic of linear simulation :
Linear |
Non-Linear |
Ratio |
\(B_{z \, linear} = -0.924 \, T\) |
\(B_{z \, non \, linear} = -0.788 \, T\) |
\(\frac{B_{z \, non \, linear}}{B_{z \, linear}} = 0.923\) |
12.2. Intensity \(I\)
.png)
Intensity \(I (A)\)
|
We can see, the intensity of non-linear simulation is less than the intensity of linear simulation :
Linear |
Non-Linear |
Ratio |
\(I_{linear} = 133.7 \, kA\) |
\(I_{non \, linear} = 113.7 \, kA\) |
\(\frac{I_{non \, linear}}{I_{linear}} = 0.851\) |
12.3. Resistance \(R\)
.png)
Resistance \(R (Ohm)\)
|
We can see, the resitance of non-linear simulation is great than the resistance of linear simulation :
Linear |
Non-Linear |
Ratio |
\(R_{linear} = 11.96 \, picoOhm\) |
\(R_{non \, linear} = 14.05 \, picoOhm\) |
\(\frac{R_{non \, linear}}{R_{linear}} = 1.17\) |
|
\(\left(\frac{R_{non \, linear}}{R_{linear}} \right)^{-1} = 0.853\), it’s the ratio of intensity. It’s normal : The Ohm law \(\ U = R \, I\) gives :
\[\begin{eqnarray*}
\frac{U}{U} = \frac{R_{non \, linear} \, I_{non \, linear}}{R_{linear} \, I_{linear}} \\
\left(\frac{R_{non \, linear}}{R_{linear}} \right)^{-1} = \frac{I_{non \, linear}}{I_{linear}}
\end{eqnarray*}\]
|
12.4. Temperature \(T\)
.png)
Temperature \(\mathbf{T} (K)\) on Or axis
|
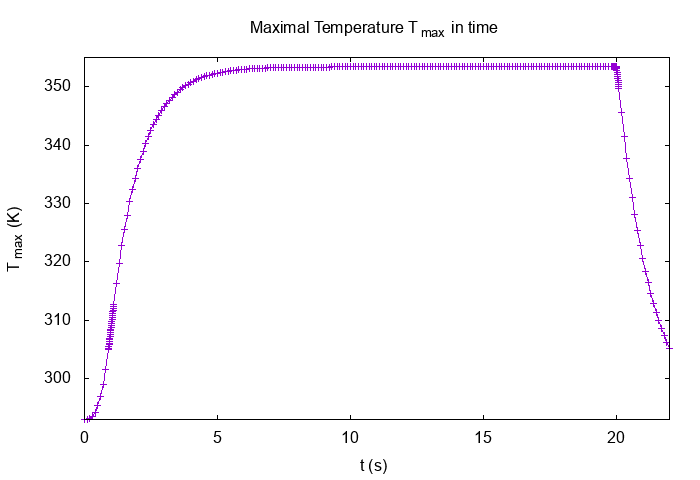
.png)
Maximal Temperature \(T_{max} (K)\)
|
We can see, the temperature of non-linear simulation is less than the temperature of linear simulation :
Linear |
Non-Linear |
Ratio |
\(T_{max \, linear} = 364.4 \, K\) |
\(T_{max \, non \, linear} = 353.3 \, K\) |
\(\frac{T_{max \, non \, linear}}{T_{max \, linear}} = 0.969\) |
12.5. Interpretation
On simulation, the temperature increases, thus the resistance (or resistivity) increases, thus the intensity (by Ohm law) and magnetic field is less than the linear case.
Moreover, if the intensity is less, the energy released by Joule’s effect is less. And, the thermal conductivity increases. This two phenomenas give that the temperature of non-linear case is less than linear case.
A non-linear matter is more resistive, thus give less intensity for same tension, but it releases less heat for the same tension.
But, what happens if we compare the two case with the same intensity.
I write python3’s script with feelpp module which permits to execute feelpp code with python3 for the linear (thermo-mag.py) case and non-linear case (non-linear.py).
| I run the static case because I have a problem to run the stationnary case with python. |
Those scripts search the tension \(U\) associated to the desired intensity \(I_0\) and simulate the associated problem. So the algorithm is :

|
We can represent this algorithm by diagram :
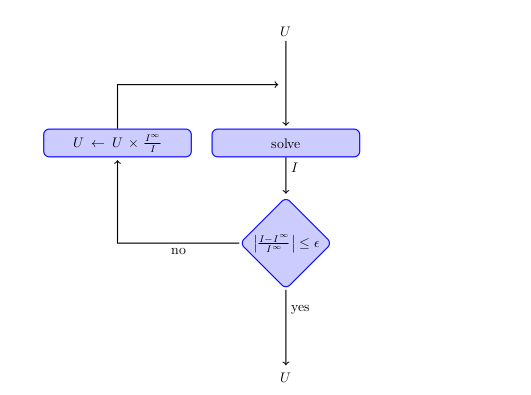
"Diagram of search of Tensions
|
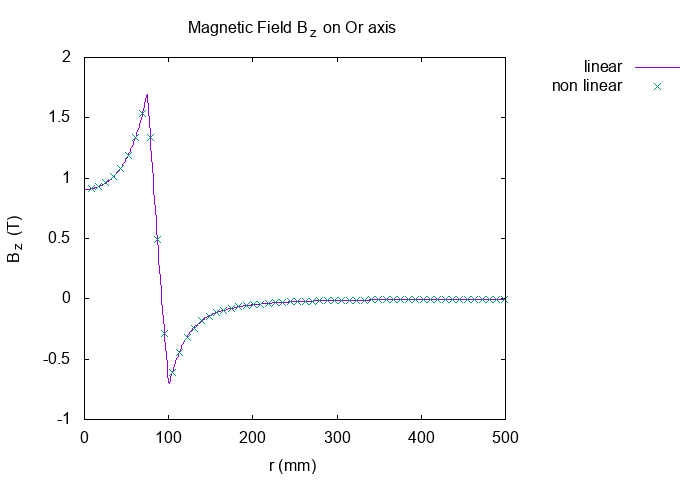
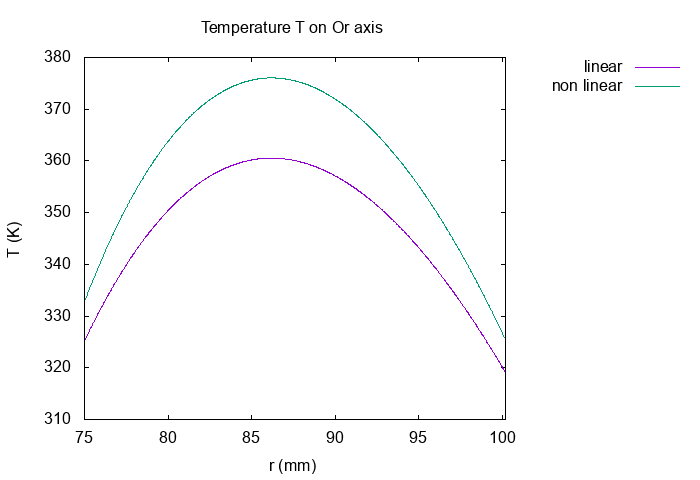
Result for desired intensity \(I=130000 \, A\) and initial tension \(U = 1 \, Volt\) :
Physics |
Linear |
Non-Linear |
\(U\) |
\(-0.9723 \, Volt\) |
\(-1.145 \, Volt\) |
\(T_{max}\) |
\(357.9 \, K\) |
\(368.8 \, K\) |
\(R\) |
\(11.95 \, picoOhm\) |
\(14.09 \, picoOhm\) |
\(B_z(0,0)\) |
\(0.906 \, T\) |
\(0.906 \, T\) |
|
|
We can see, to have the same intensity with linear problem, we need increase the tension of non-linear problem. We obtain the same magnetic field but the temperature increases.