Test of Maxwell Quasi Static with gauge condition on Two Torus

1. Introduction

In this page, I present the test case of Maxwell Quasi Static Problem with the A-V Formulation with gauge condition for a geometry of torus surrounded by air.

2. Run the calculation

The command line to run this case is :

    mpirun -np 32 feelpp_toolbox_coefficientformpdes --config-file=mqs.cfg --cfpdes.gmsh.hsize=5e-3

3. Data Files

The case data files are available in Github here :

CFG file - Edit the file
JSON file - Edit the file
GEO file - Edit the file

4. Equation

Thus \(\Omega\) the domain, comprising the conductor (or superconductor) domain \(\Omega_c\) and non conducting materials \(\Omega_n\) (\(\mathbf{J} = 0\)) like air. Let \(\Gamma = \partial \Omega\) the bound of \(\Omega\), \(\Gamma_c = \partial \Omega_c\) the bound of \(\Omega_c\), \(\Gamma_D\), \(\Gamma_{Dc}\) the bound with Dirichlet boundary condition and \(\Gamma_N\), \(\Gamma_{Nc}\) the bound with Neumann boundary condition, such that \(\Gamma = \Gamma_D \cup \Gamma_N\) and \(\Gamma_c = \Gamma_{Dc} \cup \Gamma_{Nc}\).

We introduce :

Magnetic potential field \(\mathbf{A}\) : the magnetic field writes \(\textbf{B} = \nabla \times \textbf{A}\)
Electric potential scalar : \(\nabla V = - \textbf{E} - \frac{d \textbf{A}}{d t}\)

We have the conditions :

\(\nabla \cdot \mathbf{A} = 0\)
\(\mu\) is independant of space

We want to resolve the electromagnetism problem ( with \(\mathbf{A}\) and \(V\) the unknows) :

A-V Formulation with gauge condition

\[\text{(AV+gauge)} \left\{ \begin{matrix} \sigma \frac{d \textbf{A}}{d t} + \frac{1}{\mu} \Delta \textbf{A} &=& - \sigma \nabla V & \text{ on } \Omega & \text{(AV+gauge-1)} \\ \nabla \cdot \left( \sigma \nabla V \right) &=& - \nabla \cdot \left( \sigma \frac{d \mathbf{A}}{d t} \right) & \text{ on } \Omega_c & \text{(AV'-2)} \\ \mathbf{A} \times \mathbf{n} &=& 0 & \text{ on } \Gamma_D & \text{(DA)} \\ \left( \nabla \times \mathbf{A} \right) \times \mathbf{n} &=& 0 & \text{ on } \Gamma_N & \text{(NA)} \\ V &=& V_d & \text{ on } \Gamma_{Dc} & \text{(DV)} \\ \frac{\partial V}{\partial \mathbf{n}} &=& 0 & \text{ on } \Gamma_{Nc} & \text{(NV)} \end{matrix} \right.\]

This equation is obtain from the A-V Formulation with the gauge conditions. The detail calculus are in page MQS + gauge condition.

5. Geometry

The geometry is two tores of conductor surrounded by air.

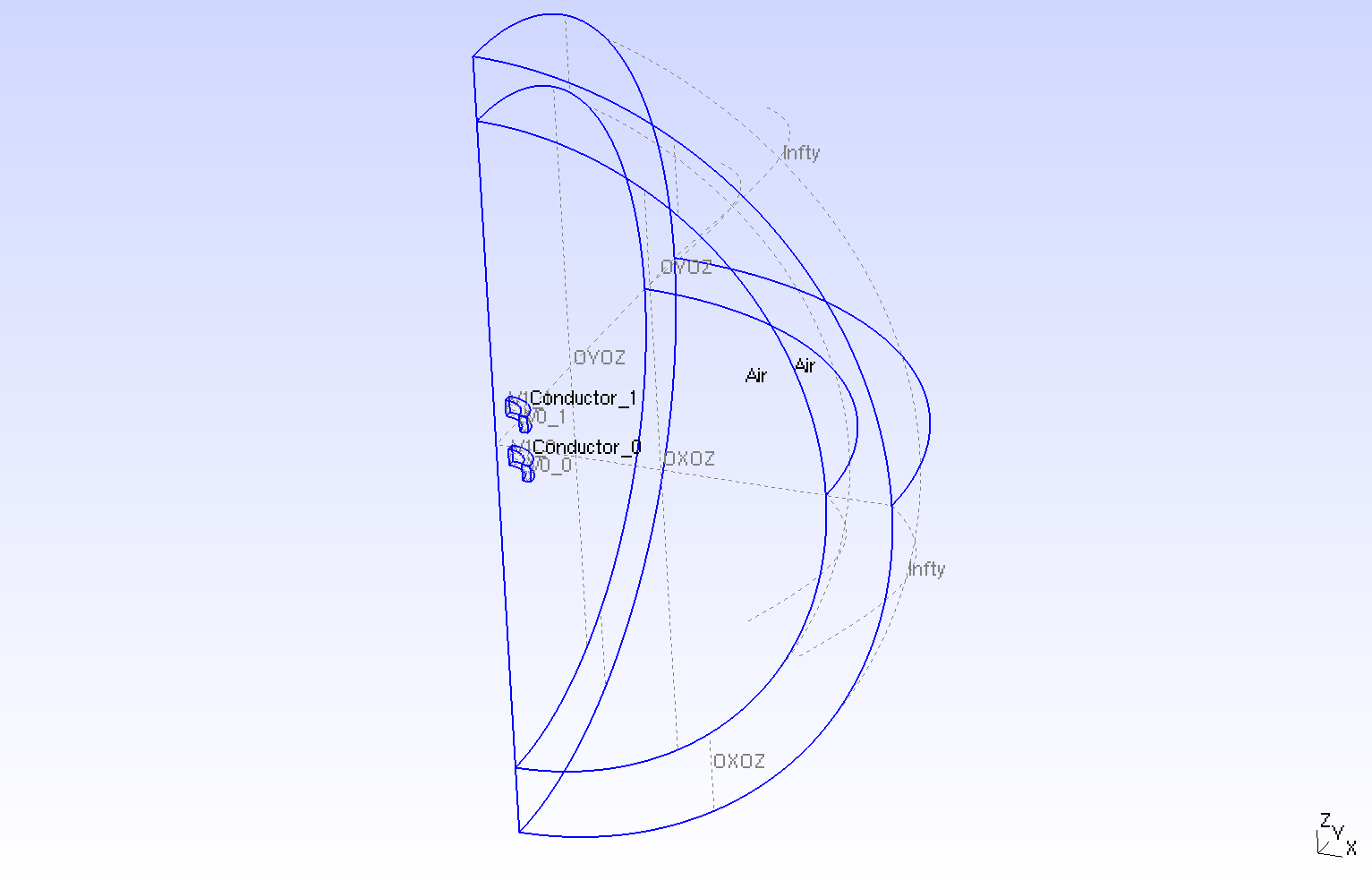
Geometry

Geometry loop on Conductors

The geometrical domains are :

Conductor_0 : the first torus, it is composed of conductive materials
- V0_0 : enter of electrical potential
- V1_0 : exit of electrical potential
Conductor_1 : the second torus, it is composed of conductive materials
- V0_1 : enter of electrical potential
- V1_1 : exit of electrical potential

( Conductor_0 \(\cup\) Conductor_1 \( = \Omega_c\) and V0_0 \(\cup\) V1_0 \(\cup\) V0_1 \(\cup\) V1_1 \( = \Gamma_{Dc}\))

air (\(\Omega/\Omega_c\)) : the air surround Conductor
- OXOZ : \(OxOz\) plan
- OYOZ : \(OyOz\) plan
- Infty : the rest of bound of Air

Symbol

Description

value

unit

\(r_{int}\)

interior radius of tores

\(75e-3\)

\(r_{ext}\)

exterior radius of tores

\(100.2e-3\)

\(z_1\)

half-height of torus

\(25e-3\)

\(r_{infty}\)

radius of infty border

\(5*r_{ext}\)

6. Initial/Boundary Conditions

We impose the Dirichlet boundary conditions :

For \(V\) equation :
- On V0_0 and V0_1 : \(V=0\)
- On V1_0 : \(V = \frac{1}{4} \left\{ \begin{matrix} \frac{t}{0.1} \text{ on } 0s \leq t < 0.1s \\ 1 \text{ on } 0.1s \leq t < 0.5s \\ t \text{ on } 0.5s \leq t \end{matrix} \right. \)
- On V1_1 : \(V = \frac{1}{4} \left\{ \begin{matrix} \frac{t}{0.1} \text{ on } 0s \leq t < 0.1s \\ 1 \text{ on } 0.1s \leq t < 0.7s \\ t \text{ on } 0.7s \leq t \end{matrix} \right. \)
For \(\mathbf{A}\) :
- On OXOZ, V0_0 and V0_1 : \(A_x = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OXOZ and V0
- On OYOZ, V1_0 and V1_1 : \(A_y = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OYOZ and V1
- Infty : We approximate the problem, Infty is the physical infty thus \(\mathbf{B}=0\) at Infty thus \(\mathbf{A} = 0\).

We initialize at \(t=0s\) :

\(V = 0\)
\(\mathbf{A} = 0\)

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file

    "BoundaryConditions":
    {
        "magnetic":
        {
            "Dirichlet":
            {
                "Infty":
                {
                    "expr":"{0,0,0}"
                }
            },
            "Dirichlet_x":
            {
                "mydir_x":
                {
                    "markers":["V0_0","V0_1","OXOZ"],
                    "expr":0
                }
            },
            "Dirichlet_y":
            {
                "mydir_y":
                {
                    "markers":["V1_0","V1_1","OYOZ"],
                    "expr":0
                }
            },
            "Dirichlet_z":
            {
                "mydir_z":
                {
                    "markers":["V0_0","V0_1","OXOZ","V1_0","V1_1","OYOZ"],
                    "expr":0
                }
            }
        },
        "electric":
        {
            "Dirichlet":
            {
                "V0_0":
                {
                    "expr":"materials_Conductor_0_V0:materials_Conductor_0_V0"
                },
                "V0_1":
                {
                    "expr":"materials_Conductor_1_V0:materials_Conductor_1_V0"
                },
                "V1_0":
                {
                    "expr":"materials_Conductor_0_V1:materials_Conductor_0_V1"
                },
                "V1_1":
                {
                    "expr":"materials_Conductor_1_V1:materials_Conductor_1_V1"
                }
            }
        }
    }

For initial condition, we write nothing in JSON, by default the application put zeros on initialization.

7. Weak Formulation

The weak formulation of A-V Formulation + gauge is :

\[\text{(AV+gauge Weak)} \left\{ \begin{eqnarray*} \int_{\Omega}{ \sigma \frac{d \mathbf{A}}{d t} \mathbf{ϕ} } + \int_{\Omega}{ \frac{1}{\mu} \nabla \mathbf{A} \cdot \nabla \mathbf{ϕ} } &=& - \int_{\Omega_c}{\sigma \nabla V \, \mathbf{ϕ}} \\ \int_{\Omega_c}{ \sigma \nabla V \cdot \nabla \psi } &=& - \int_{\Omega_c}{\sigma \frac{d \mathbf{A}}{d t} \cdot \nabla \psi} \end{eqnarray*} \right.\]

8. Parameters

The parameters of problem are :

On Conductor :

Symbol

Description

Value

Unit

\(V0\)

scalar electrical potential on V0

\(0\)

\(Volt\)

\(V1\)

scalar electrical potential on V1

\(\frac{1}{4} \left\{ \begin{matrix} t \ \text{on} \ 0s \leq t < 1s \\ 1 \ \text{on} \ 1s \leq t < 20s \\ 0 \ \text{on} \ 20s \leq t \end{matrix} \right.\)

\(Volt\)

\(\sigma\)

electrical conductivity

\(58e6\)

\(S/m\)

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

On Air :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

9. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficient associate to Weak Formulation are :

In the json file, we note magnetic the equation (AV'-1) and electric the equation (AV'-2).

On Conductor_0 and Conductor_1 :

Coefficient

Description

Expression

magnetic_d

damping or mass coefficient

\(\sigma\)

magnetic_c

diffusion coefficient

\(\frac{1}{\mu}\)

magnetic_f

source term

\(- \sigma \nabla V \)

electric_c

damping or mass coefficient

\(\sigma\)

electric_gamma

source term

\(\sigma \, \frac{d \mathbf{A}}{d t}\)

On Air (the lectrical potential isn’t computed on Air) :

Coefficient

Description

Expression

magnetic_c

diffusion coefficient

\(\frac{1}{\mu}\)

On JSON file, the coefficients are writed :

CFPDEs coefficients on JSON file

    "Materials":
    {
        "Conductor_0":
        {
            "V0":0,
            "V1":"1/4*(t/(0.1)*(t<(0.1))+(t<(0.5))*(t>(0.1))):t",
            "sigma":58e6,       // S.m-1
            "mu":"4*pi*1e-7",   // kg.m/A2/S2

            "magnetic_d":"sigma:sigma",
            "magnetic_c":"1/mu:mu",
            "magnetic_f":"{-sigma*electric_grad_V_0,-sigma*electric_grad_V_1,-sigma*electric_grad_V_2}:sigma:electric_grad_V_0:electric_grad_V_1:electric_grad_V_2",

            "electric_c":"sigma:sigma",
            "electric_gamma":"{sigma*magnetic_dA_dt_0,sigma*magnetic_dA_dt_1,sigma*magnetic_dA_dt_2}:sigma:magnetic_dA_dt_0:magnetic_dA_dt_1:magnetic_dA_dt_2"
        },
        "Conductor_1":
        {
            "V0":0,
            "V1":"1/4*(t/(0.1)*(t<(0.1))+(t<(0.7))*(t>(0.1))):t",
            "sigma":58e6,       // S.m-1
            "mu":"4*pi*1e-7",   // kg.m/A2/S2

            "magnetic_d":"sigma:sigma",
            "magnetic_c":"1/mu:mu",
            "magnetic_f":"{-sigma*electric_grad_V_0,-sigma*electric_grad_V_1,-sigma*electric_grad_V_2}:sigma:electric_grad_V_0:electric_grad_V_1:electric_grad_V_2",

            "electric_c":"sigma:sigma",
            "electric_gamma":"{sigma*magnetic_dA_dt_0,sigma*magnetic_dA_dt_1,sigma*magnetic_dA_dt_2}:sigma:magnetic_dA_dt_0:magnetic_dA_dt_1:magnetic_dA_dt_2"
        },
        "Air":
        {
            "physics":"magnetic",
            "mu":"4*pi*1e-7",   // kg.m/A2/S2
            "magnetic_c":"1/mu:mu"
        }
    }

10. Numeric Parameters

This section show the parameters used to compute the simulation.

Size of mesh :
- On Conductor : \(0.5 \, mm\)
- On Infty : \(100 \, mm\)
Time Parameters :
- Time step : \(0.1 \, s\)
- Initial Time : \(0 \, s\)
- Final Time : \(22 \, s\)
Element type : \(P1\)
Solver : automatic
Number of CPU core : \(32\)

Mesh of Geometry

11. Results

11.1. Magnetic Fields

I plot the horizontal magnetic field by time on point \((0,0,0)\).

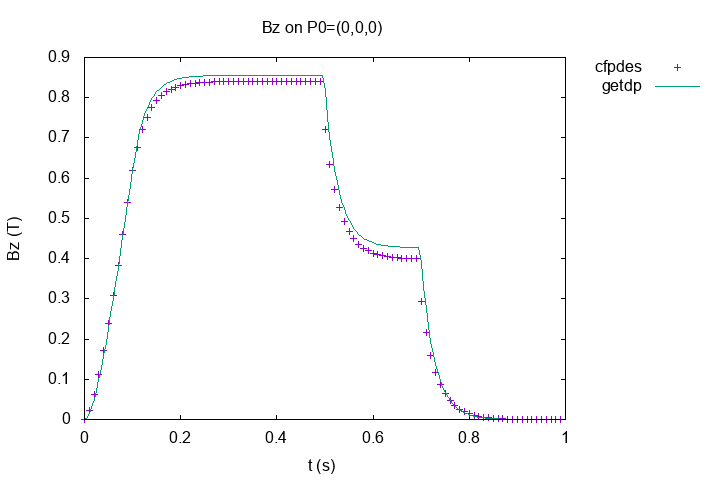
Horizontal Magnetic Field \(B_z (T)\) by time

We can see the four step :

the ramp for the two tensions
the tray for the two tensions
the tray for the tension \(U_1\) and the tray at 0 for the tension \(U_0\)
the tray for the tray at 0 for the tensions \(U_0\) and \(U_1\)

11.2. Intensities

The analytical solve of intensities is computed by python3’s script : Edit the file, with the formula :

\[\small{ \mathbf{I}(t) = \left\{ \begin{matrix} \left( t \, \left( \mathbf{R} \mathbf{L}^{-1} \right)^{-1} - \left( \mathbf{R} \mathbf{L}^{-1} \right)^{-2} \left( Id - e^{-\mathbf{R} \mathbf{L}^{-1} t} \right) \right) \ \mathbf{L}^{-1} \, \begin{pmatrix} 1/0.1 \\ 1/0.1 \end{pmatrix} & 0s \leq t \leq 0.1s \\ e^{-\mathbf{R} \mathbf{L}^{-1} t} \, \mathbf{C}_1 + \mathbf{R}^{-1} \begin{pmatrix} 1 \\ 1 \end{pmatrix} & 0.1s \leq t \leq 0.5s \\ e^{-\mathbf{R} \mathbf{L}^{-1} t} \, \mathbf{C}_2 + \mathbf{R}^{-1} \begin{pmatrix} 0 \\ 1 \end{pmatrix} & 0.5s \leq t \leq 0.7s \\ e^{-\mathbf{R} \mathbf{L}^{-1} t} \, \mathbf{C}_3 & 0.7s \leq t \leq 1s \\ \end{matrix} \right. }\]

And the values :

Symbol

Description

Value

Unit

\(R_0\)

resistance of Conductor_0

\(7.479339e-06\)

\(Ohm\)

\(R_1\)

resistance of Conductor_0

\(7.479339e-06\)

\(Ohm\)

\(L_0\)

auto-inductance of Conductor_0

\(1.920400e-07\)

\(Henry\)

\(L_0\)

auto-inductance of Conductor_0

\(1.920400e-07\)

\(Henry\)

\(M_{01}\)

inductance from Conductor_0 to Conductor_1

\(1.705000e-08\)

\(Henry\)

\(M_{10}\)

inductance from Conductor_1 to Conductor_0

\(1.705000e-08\)

\(Henry\)

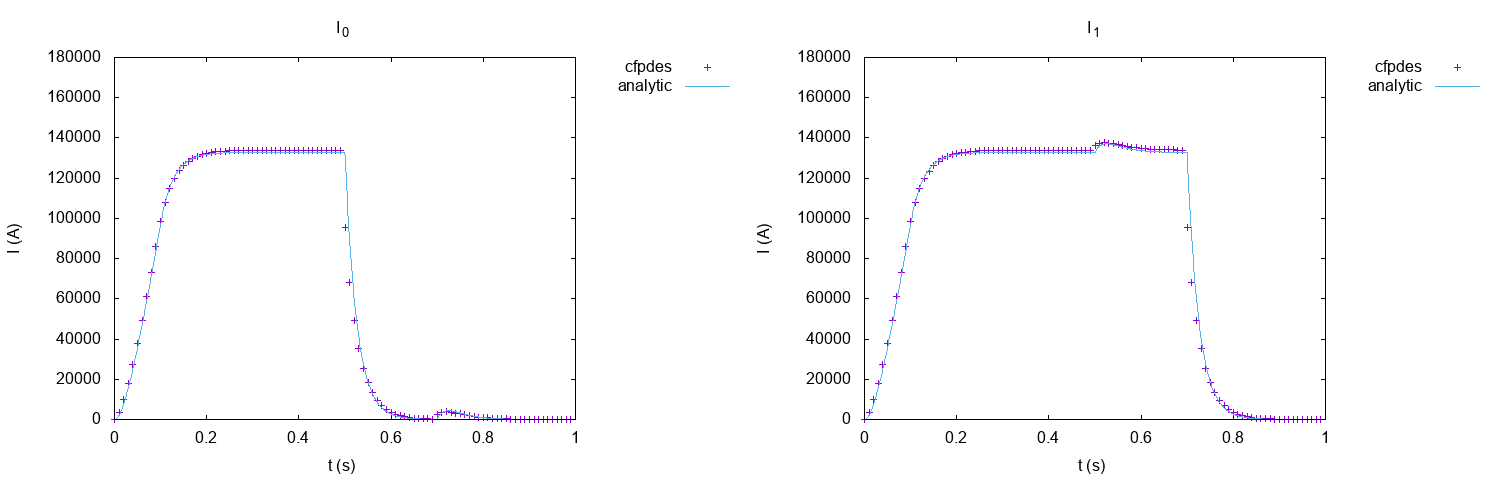
Intensities : Comparison between numerical and analytical results

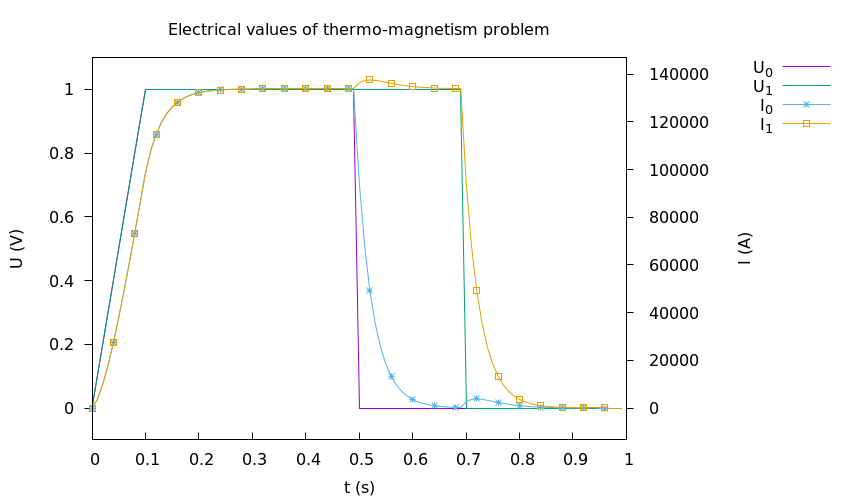
Figure 1. Intensities \(I_i (A)\) and Tensions \(U_i(V)\), caption=

The intensities follow the tensions like for 1-Torus problem with the four step (ramp, trays and cuts). But, we can see little peaks. This peak on one intensity appears when the tension of other conductor is cut. This phenomena is called Electromagnetism Induction.

The Electromagnetism Induction is the production of an electromotive force across an electrical conductor in a changing magnetic field.

With the equation of Maxwell-Faraday :

\[ \nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}\]

We can see, with time variation of magnetic field \(\mathbf{B}\), we have creation of electrical field. For us case, when we cut the tension for one conductor, we have great time variation of magnetic field thus the other conductor answer by Maxwell-Faraday equation with creation of electrical field and current. When the magnetic field is at zeros, is phenomena disapears.