Axisymmetrical Geometry
This page explain what is a axisymmetrical Geometry.
The axisymmetrical coordinates is usefull on my intership to reduce the complexity of problem : reduce the dimension to 3 to 2 thus reduce the time of compute of my simulation.
We can see a study of efficiency of passage to axisymmetrical compute for heat problem Comparison with Three Dimensions.
1. Cartesian Coordinates
The Cartesian coordinates are the most common coordinates used to describe a geometry. It composed by three coordinates :
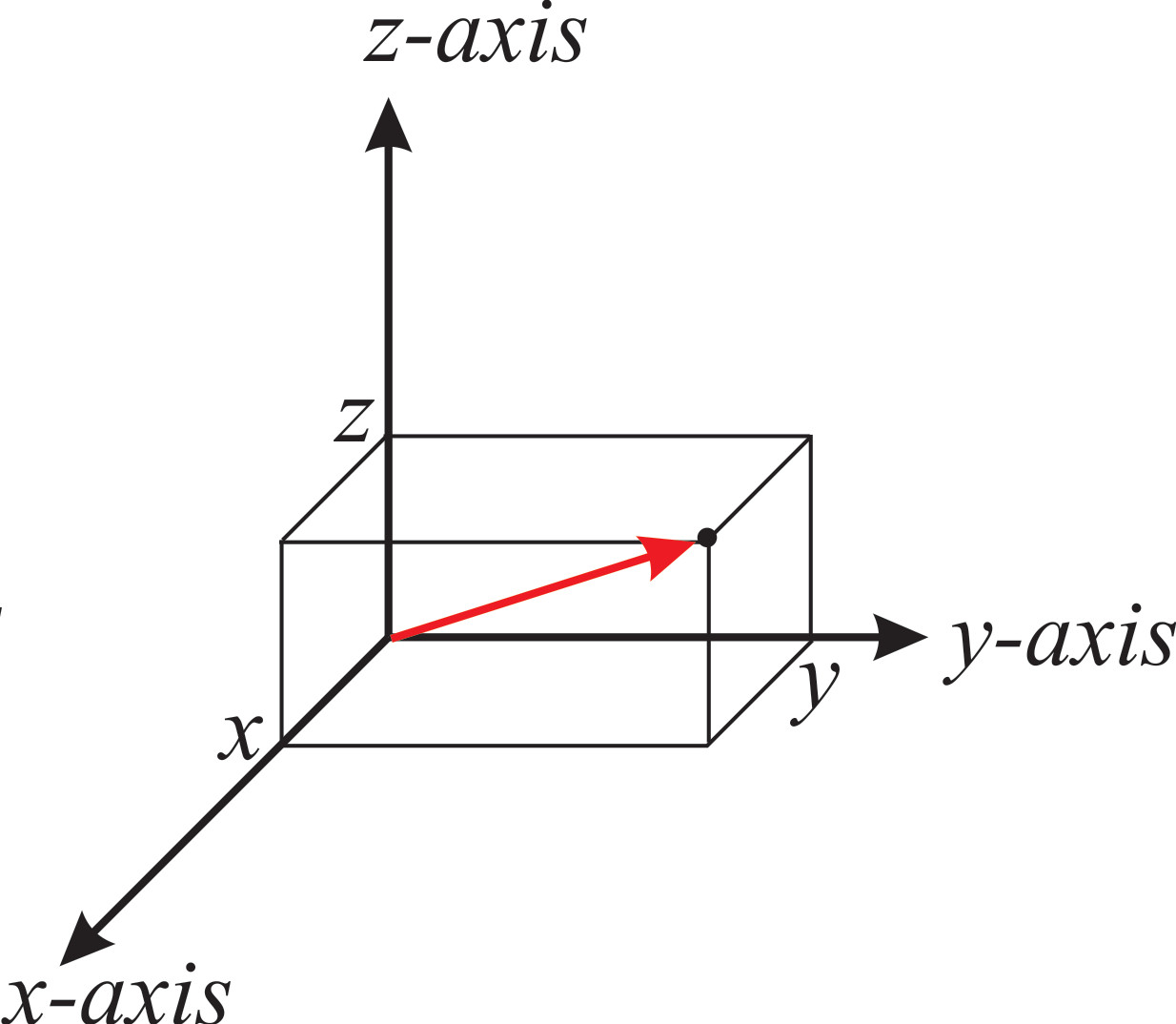
Schema of cartesian coordinates
|
The cartesian basis vector is :
2. Cylindrical Coordinates
We can use an other system of coordinates to describes a point on \(\mathbb{R}^3\), cylindrical coordinates. It composed by three coordinates \((r,\theta,z)\) :
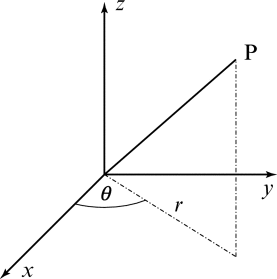
Schema of cylindrical coordinates
|
We can pass to cylinder coordinates to cartesian coordinates by changing variables :
And :
The cylinder basis vector is :
This coordinates system is usefull to describe the geometry or movement around an axis.
3. Axisymmetrical Coordinates
The axisymmetrical coordinates is an simplification of cylindrical coordinates. An geometry is considered like axisymmetrical geometry when in cylinder coordinates, the geometry is independant to \(\theta\), or the geometry is symmetrical with respect to the axis. The geometry can be describe with a plan \(O_{rz}\), all point are described by \((r,z)\) :
The axisymmetric basis vector is :
For example, a cylinder can be represent by a rectangle on axisymmetrical coordinates.
We can see the axisymmetrical plan \(O_{rz}\) like a cut a geometry along a transverse axis.
The interest to this system of coordinates is to reduce the dimensions of geometry and simplificate the problem.