Test case of Thermo-Magnetism with Non-Linear Coefficients in Three Dimensions

1. Introduction

In previous page (Test Case in Three Dimensions with Linear Coefficients and Test Case in Axisymmetric with Linear Coefficients), I present the resolution of thermo-magnetism problem with cLinear Coefficients (electrical and thermal conductivity are constants). But in reality it isn’t the case, the coefficients depend of temperature.

This page presents the simulation of electromagnetism equation (A-V Formulation) coupled with heat equation with non-linear coefficients on geometry of torus in transient case.

2. Run the calculation

The command line to run this case is :

    mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=non-linear.cfg --cfpdes.gmsh.hsize=1e-4

To run the case with adaptative time-step :

    sh feelpp_adaptative.sh

3. Data Files

The case data files are available in Github here :

CFG file - Edit the file
JSON file - Edit the file
GEO file - Edit the file
SH script for adaptative time-step - Edit the file

4. Equation

In this subsection, we retake the coupled equation (AV+Heat Axis) of Heat equation and AV-Formulation in axisymetrical coordinates with new coefficients.

The domain of resolution of electromagnetism part is \(\Omega^{axis}\) with bounds \(\Gamma^{axis}\), \(\Gamma_D^{axis}\) the bound of Dirichlet conditions and \(\Gamma_N^{axis}\) the bound of Neumann conditions such that \(\Gamma^{axis} = \Gamma_N^{axis} \cup \Gamma_D^{axis}\).

The domain of resolution of heat part is \(\Omega_c^{axis} \subset \Omega^{axis}\) (and the domain of definition of electrical potential \(V\) and electrical conductivity \(\sigma\)) with bounds \(\Gamma_c^{axis}\), \(\Gamma_{Dc}^{axis}\) the bound of Dirichlet conditions and \(\Gamma_{Nc}^{axis}\) the bound of Neumann conditions such that \(\Gamma_c^{axis} = \Gamma_{Nc}^{axis} \cup \Gamma_{Dc}^{axis}\).

Moreover, the electrical conductivity and thermal conductivity for metal can exprim with emprical law :

The resistivity \(\rho\) increase linearly with the temperature such that :

\[ \rho(T) = \rho_0 \, \left( 1 + \alpha (T-T_0) \right)\]

With \(\rho_0\) the resistivity at reference temperature \(T_0\) and \(\alpha\) the temperature coefficient obtained empirically.

Thus the electrical condutivity becomes :

\[ \sigma(T) = \frac{\sigma_0}{1+\alpha (T-T_0)}\]

With \(\sigma_0 = \frac{1}{\rho_0}\) the electrical conductivity at reference temperature \(T_0\).

Moreover, the thermal conductivity of metal is proportionnal to its electrical conductivity and its temperature, it’s the Wiedemann-Franz law :

\[ k(T) = \sigma(T) \, L \, T\]

With \(L\) the constant of Lorentz number and is proper of materials.

But, we can rewrite this law :

\[ k(T) = \frac{k_0}{1+\alpha (T-T_0)} \frac{T}{T_0}\]

With thermal conductivity \(k_0\) at reference temperature.

Differential Formulation in Axisymmetric

\[\text{(AV+Heat Axis)} \left\{ \begin{matrix} \sigma(T) \, \frac{\partial \Phi}{\partial t} - \frac{1}{\mu} \Delta \Phi + \frac{2}{\mu \, r} \frac{\partial \Phi}{\partial r} + \sigma(T) \, \frac{\partial V}{\partial \theta} = 0 & \text{ on } \Omega^{axis} & \text{(AV-1 Axis)} \\ V = \frac{U}{2\pi} \, \theta & \text{ on } \Omega_c^{axis} \\ A_{\theta} = 0 & \text{ on } \Gamma_D^{axis} & \text{(D Axis)} \\ \frac{\partial A_{\theta}}{\partial \mathbf{n}^{axis}} = 0 & \text{ on } \Gamma_N^{axis} & \text{(N Axis)} \\ \rho C_p \, \frac{\partial T}{\partial t} - k(T) \, \Delta T = \sigma \, \left( \frac{1}{r} \, \frac{\partial V}{\partial \theta} + \frac{\partial A_{\theta}}{\partial t} \right)^2 & \text{ on } \Omega_c^{axis} & \text{(Heat Axis)} \\ \frac{\partial T}{\partial \mathbf{n}^{axis}} = 0 & \text{ on } \Gamma_{Nc}^{axis} & \text{(Nc Axis)} \\ - k(T) \, \frac{\partial T}{\partial \mathbf{n}^{axis}} = h \, \left( T - T_c \right) & \text{ on } \Gamma_{Rc}^{axis} & \text{(Rc Axis)} \end{matrix} \right.\]

With :

\(\Phi = r \, A_{\theta}\), with magnetic potential field \(\mathbf{A} = \begin{pmatrix} A_r \\ A_{\theta} \\ A_z \end{pmatrix}_{cyl}\) such that the magnetic field is writed \(\mathbf{B} = \nabla \times \mathbf{A}\)
\(T\) : temperature \((K)\)
\(\sigma = \frac{\sigma_0}{1 + \alpha \, \left( T - T_0 \right)}\) : electric conductivity \((S/m)\)
- \(\sigma_0\) electrical conductivity at reference temperature \(T_0\)
- \(\alpha\) temperature coefficient
\(\mu\) : electric permeability \((kg/A^2/S^2)\)
\(\rho\) : density \((kg/m^3)\)
\(C_p\) : thermal capacity \((J/K/kg)\)
\(k = \frac{k}{1 + \alpha \, \left( T - T_0 \right)} \, \frac{T}{T_0}\) : thermal conductivity \((W/m/K)\)
- \(k_0\) thermal conductivity at reference temperature \(T_0\)
- \(\alpha\) temperature coefficient
\(U\) : tension \(Volt\)

The equation become coupled in both senses, the first equation (AV-1 Axis) depends of temperature \(T\) and the second equation (Heat Axis) depends on \(A_{\theta}\).

5. Geometry

The geometry is a torus of the conductor in cartesian coordinates \((x,y,z)\), surrounded by air.

Geometry in three dimensions

Geometry in three dimensions loop on Conductor

The geometrical domains are :

Conductor (\(\Omega_c\)) : the torus, it is composed of conductive materials
- V0 : enter of electrical potential
- V1 : exit of electrical potential

(V0 \(\cup\) V1 \( = \Gamma_{Dc}\))

air (\(\Omega/\Omega_c\)) : the air surround Conductor
- OXOZ : \(OxOz\) plan
- OYOZ : \(OyOz\) plan
- Infty : the rest of bound of Air

Symbol

Description

value

unit

\(r_{int}\)

interior radius of torus

\(75e-3\)

\(r_{ext}\)

exterior radius of torus

\(100.2e-3\)

\(z_1\)

half-height of torus

\(25e-3\)

\(r_{infty}\)

radius of infty border

\(5*r_{ext}\)

6. Initial/Boundary Conditions

We impose the Dirichlet boundary conditions :

For electrical potential scalar \(V\) :
- On V0 : \(V=0\)
- On V1 : \(V=1\)
For magnetic potential field \(\mathbf{A}\) :
- On OXOZ and V0 : \(A_x = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OXOZ and V0
- On OYOZ and V1 : \(A_y = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OYOZ and V1
- Infty : We approximate the problem, Infty is the physical infty thus \(\mathbf{B}=0\) at Infty thus \(\mathbf{A} = 0\).
For temperature \(T\) :
- On V0, V1, Upper and Bottom we put Neumann condition \(\frac{\partial T}{\partial \mathbf{n}} = 0\)
- On Interior and Exterior, we put Robin condition \(k \frac{\partial T}{\partial \mathbf{n}} = h \, \left( T - T_c \right)\). It represents the cooling by water.

We initialize at \(t=0s\) :

\(V = 0\)
\(\mathbf{A} = 0\)
\(T = T_i\)

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file

    "BoundaryConditions":
    {
        "magnetic":
        {
            "Dirichlet":
            {
                "Infty":
                {
                    "expr":"{0,0,0}"
                }
            },
            "Dirichlet_x":
            {
                "magdirx":
                {
                    "markers":["V0","OXOZ"],
                    "expr":"0"
                }
            },
            "Dirichlet_y":
            {
                "magdiry":
                {
                    "markers":["V1","OYOZ"],
                    "expr":"0"
                }
            },
            "Dirichlet_z":
            {
                "magdirz":
                {
                    "markers":["V0","OXOZ","V1","OYOZ"],
                    "expr":"0"
                }
            }
        },
        "electric":
        {
            "Dirichlet":
            {
                "V0":
                {
                    "expr":"V0:V0"
                },
                "V1":
                {
                    "expr":"V1:V1"
                }
            }
        },
        "heat":
        {
            "Robin":
            {
                "heatrobin":
                {
                    "markers":["Interior","Exterior"],
                    "expr1":"h:h",
                    "expr2":"h*T_c:h:T_c"
                }
            }
        }
    }

On JSON file, the intial conditions are writed : .Initial conditions on JSON file

    "InitialConditions":
    {
        "temperature":
        {
            "Expression":
            {
                "Conductor":
                {
                    "expr":"T_i:T_i"
                }
            }
        }
    }

7. Weak Formulation

We obtain :

Weak Formulation

\[\scriptsize{ \text{(Weak Thermo-Mag Axis)} \left\{ \begin{eqnarray*} \int_{\Omega}{ \sigma \frac{d \mathbf{A}}{d t} \mathbf{ϕ} } + \int_{\Omega}{ \frac{1}{\mu} \nabla \mathbf{A} \cdot \nabla \mathbf{ϕ} } &=& - \int_{\Omega_c}{\sigma \nabla V \, \mathbf{ϕ}} \\ \int_{\Omega_c}{ \sigma \nabla V \cdot \nabla \psi } &=& - \int_{\Omega_c}{\sigma \frac{d \mathbf{A}}{d t} \cdot \nabla \psi} \int_{\Omega_c}{ \rho C_p \, \frac{\partial T}{\partial t} \, \phi } + \int_{\Omega_c}{ k \, \nabla T \cdot \nabla \phi } = \int_{\Omega_c}{ Q \, \phi } - \int_{\Gamma_{Rc}}{ h \, (T-T_c) \, \phi } \end{eqnarray*} \right. }\]

8. Parameters

The parameters of problem are :

On Conductor :

Symbol

Description

Value

Unit

\(V_0\)

scalar electrical potential on V0

\(0\)

\(Volt\)

\(V_1\)

scalar electrical potential on V0

\(\frac{1}{4}\)

\(Volt\)

\(\sigma\)

electrical conductivity

\(4.8e7\)

\(S/m\)

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

\(k\)

thermal conductivity

\(380\)

\(W/m/K\)

\(C_p\)

thermal capacity

\(380\)

\(J/K/kg\)

\(\rho\)

density

\(10000\)

\(kg/m^3\)

\(h\)

convective coefficient

\(80000\)

\(W/m^2/K\)

\(T_c\)

cooling temperature

\(293\)

\(K\)

\(T_i\)

initial temperature

\(293\)

\(K\)

On Air :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

On JSON file, the parmeters are writed :

Parameters on JSON file

    "Parameters":
    {
        "V0":0,
        "V1":"1/4*(t/1.*(t<1.)+(t>1.)*(t<5.5)):t",

        "h":80000,  // W/m2/K
        "T_c":293,  // K
        "T_i":293   // K
    }

9. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficients associate to Weak Formulation are :

For Magnetic equation of unknow \(\mathbf{A}\) :
- On Conductor :
Coefficient

Description

Expression

\(d\)

damping or mass coefficient

\(\sigma\)

\(c\)

diffusion coefficient

\(\frac{1}{\mu}\)

\(f\)

source term

\(- \sigma \, \nabla V\)
- On Air :
Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\frac{r}{\mu}\)
For Electric equation of unknow \(\mathbf{A}\) :
- On Conductor :
Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\sigma\)

\(\gamma\)

source term

\(\sigma \mathbf{A}\)

For heat equation (Weak Heat Axis), on Conductor (the temperature isn’t computed on Air) :

Coefficient

Description

Expression

\(d\)

damping or mass coefficient

\(\rho \, C_p\)

\(c\)

diffusion coefficient

\(k\)

\(f\)

source term

\(\sigma \, \left( \nabla V + \frac{\partial \mathbf{A}}{\partial t} \right)\)

On JSON file, the coefficients are writed :

CFPDEs coefficients on JSON file

    "Materials":
    {
        "Conductor":
        {
            "T0":293,       // K
            "alpha":3.6e-3,

            "sigma0":58e+6,  // S.m-1
            "sigma":"sigma0/(1+alpha*(heat_T-T0)):sigma0:alpha:heat_T:T0",  // S.m-1
            "mu":"4*pi*1e-7",   // kg.m/A2/S2

            "magnetic_d":"sigma:sigma",
            "magnetic_c":"1/mu:mu",
            "magnetic_f":"{-sigma*electric_grad_V_0,-sigma*electric_grad_V_1,-sigma*electric_grad_V_2}:sigma:electric_grad_V_0:electric_grad_V_1:electric_grad_V_2",

            "electric_c":"sigma:sigma",
            "electric_gamma":"{sigma*magnetic_dA_dt_0,sigma*magnetic_dA_dt_1,sigma*magnetic_dA_dt_2}:sigma:magnetic_dA_dt_0:magnetic_dA_dt_1:magnetic_dA_dt_2",

            "k0":380,        // W/m/K
            "k":"k0/(1+alpha*(heat_T-T0))*heat_T/T0:k0:alpha:heat_T:T0",        // W/m/K
            "rho":10000,    // kg/m3
            "Cp":380,       // J/K/kg

            "heat_c":"k:k",
            "heat_f":"materials_Conductor_sigma*((electric_grad_V_0+magnetic_dA_dt_0)*(electric_grad_V_0+magnetic_dA_dt_0)+(electric_grad_V_1+magnetic_dA_dt_1)*(electric_grad_V_1+magnetic_dA_dt_1)+(electric_grad_V_2+magnetic_dA_dt_2)*(electric_grad_V_2+magnetic_dA_dt_2)):materials_Conductor_sigma:electric_grad_V_0:electric_grad_V_1:electric_grad_V_2:magnetic_dA_dt_0:magnetic_dA_dt_1:magnetic_dA_dt_2",
            "heat_d":"rho*Cp:rho:Cp"
        },
        "Air":
        {
            "physics":"magnetic",
            "mu":"4*pi*1e-7",   // kg.m/A2/S2
            "magnetic_c":"1/mu:mu"
        }
    }

10. Numeric Parameters

This section show the parameters used to compute the simulation.

Size of mesh : \(5 \, mm\)
Time Parameters :
- Time step : I use adaptative time step. Near of brutal changement of current, the time step is little, in other case, the time step is big. I put adaptative time step to have good precision near of changement (cut of current at \(t=22s\)) and to not explose the time of compute. The shell script feelpp_adaptative.sh implements that.
  
  \(\Delta_t = \left\{ \begin{matrix} 0.1s \, \text{for} \, 0s<t<0.9s \\ 0.008s \, \text{for} \, 0.9s<t<1.1s \\ 0.1s \, \text{for} \, 1.1s<t<19.9s \\ 0.008s \, \text{for} \, 19.9s<t<20.1s \\ 0.1 \, \text{for} \, 20.1s<t<22s \end{matrix} \right.\)
- Initial Time : \(0 \, s\)
- Final Time : \(22 \, s\)
Element type : \(P1\) for three equation (\(\mathbf{A}\), \(V\) and \(T\))

Mesh of Geometry

11. Result

The analytical solve of potential magnetic field and magnetic field (the cyan curve on plots) is computed by python3’s module MagnetTools.MagnetTools. The module based on paper : spire.

The analytical solve of intensity (and magnetic field) is computed on python3’s script Edit the file.

11.1. Intensity

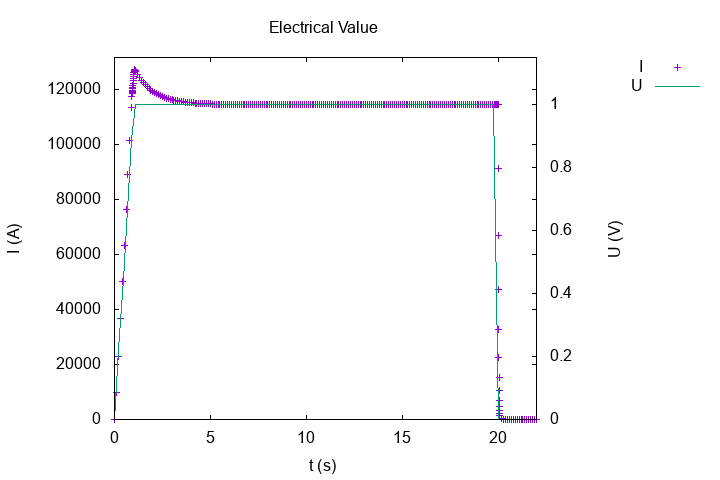
Feelpp compute in post-process, the intensity of circuit :

\[\begin{eqnarray*} I(t) &=& \int_{\Omega_c \cap OrOz}{ \mathbf{J} \cdot \mathbf{n} \ ds } \\ &=& \int_{\Omega_c^{axis}}{ \sigma \left( \frac{1}{r} \frac{U}{2\pi} + \frac{1}{r} \frac{\partial \Phi}{\partial t} \right) \, drdz } \end{eqnarray*}\]

Intensity of current \(I(A)\)

We can observe, the intensity form a peak around the first cut (betwenn ramp and tray) and the intensity stabilizes around the value \(I = 113.7 \, kA\), it is the stationnary value give by Ohm Law : \(U = R \, I\) with \(R_{non \, linear} = 14.05 \, picoOhm\).

We can explain this phenomena with plot of intensity and resistance :

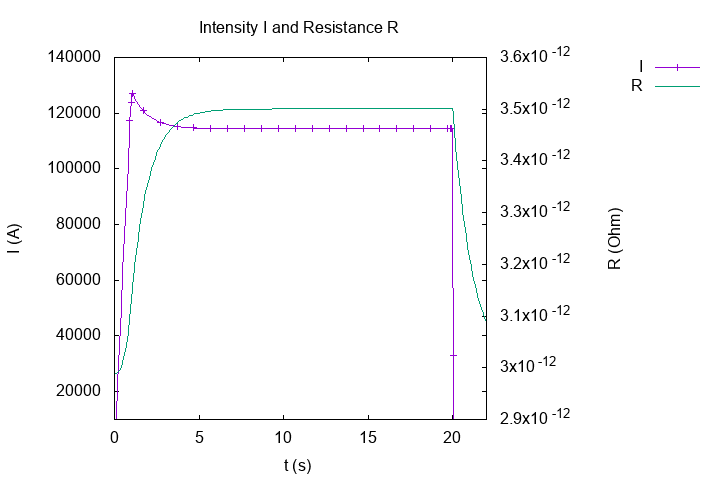
Intensity of current \(I(A)\) and Resistance \(R(Ohm)\)

The resistance increases in time because the temperature increases. In begining, the resistance is small, the intensity can have great value but after the resistance increases and the intensity by Ohm law \(U = R \, I\) (recall \(U\) is constant) decreases and stabilzes with the resistance.

11.2. Magnetic field \(B_z\)

Recall, with axisymmetric condition :

\[ \mathbf{B} = \begin{pmatrix} B_r \\ 0 \\ B_z \end{pmatrix}_{cyl} = \nabla \times \mathbf{A} = \begin{pmatrix} - \frac{\partial A_{\theta}}{\partial z} \\ 0 \\ \frac{1}{r} \frac{\partial \left( r \, A_{\theta} \right)}{\partial z} \end{pmatrix}\]

Thus \(B_z = \frac{1}{r} \frac{\partial \Phi}{\partial r} \).

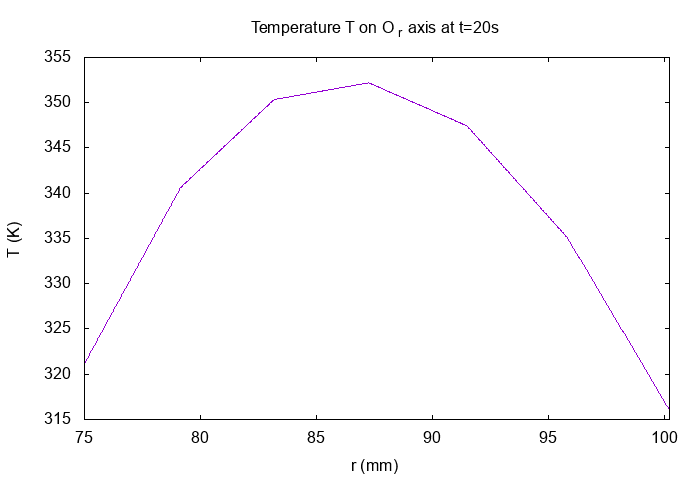
On \(Or\) axis at \(t=20s\)

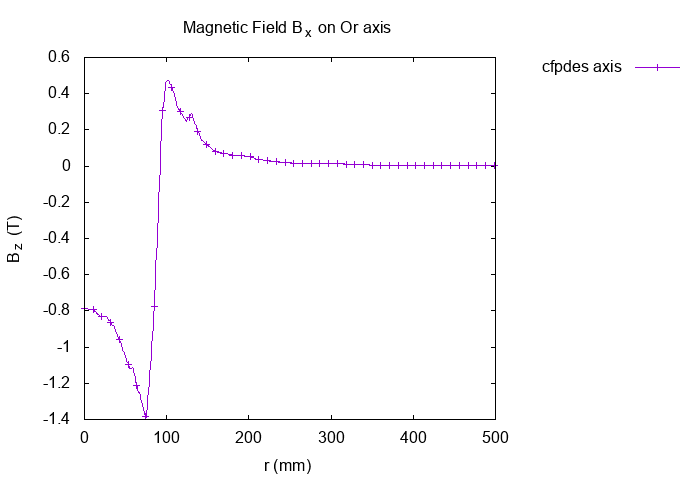
Horizontal Magnetic Field \(B_z(T)\) on Or

On origin \((0,0,0)\) across the time

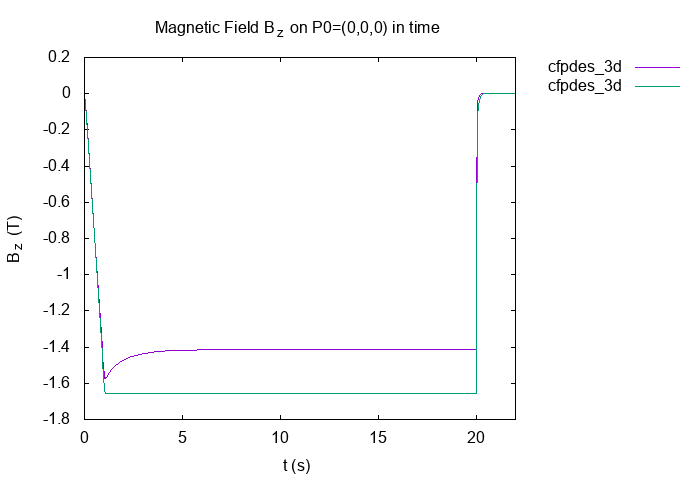
"Horizontal Magnetic Field \(B_z(T)\)

Magnetic Field across the time :

Horizontal Magnetic Field \(B_z (T)\)

11.3. Electrical value

"Some electical value \(U(V/rad),I(A)\)

11.4. Temperature \(T (K)\)

On \(Or\) axis at \(t=20s\)

Temperature \(T(K)\) on Or

On point \((r_0=0.086m,0,0)\) in time

Maximal Temperature \(T_{max} (K)\)

Temperature across the time :

Temperature \(T (K)\)

12. Comparison with Linear case

I run the simulation of thermo-magnetism problem with Linear coefficients, \(\sigma\) and \(k\) are constants :

\(\sigma = \sigma_0\)
\(k = k_0\)

If we overlap the result of Non-Linear and Linear, we have :

12.1. Magnetic Field \(\mathbf{B}\)

Magnetic Field \(\mathbf{B} (T)\) on Or axis

Magnetic Field \(\mathbf{B}(0,0,0) (T)\)

We can see, the magnetic field of non-linear simulation is less than the magnetic of linear simulation :

\(B_{z \, non \, linear} = -0.78p \, T\)
\(B_{z \, linear} = -0.924 \, T\)
\(\frac{B_{z \, non \, linear}}{B_{z \, linear}} = 0.923 \, T\)

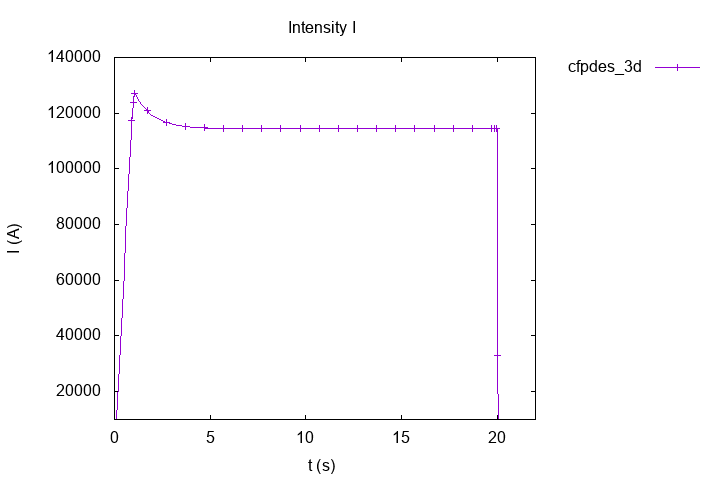
12.2. Intensity \(I\)

Intensity \(I (A)\)

We can see, the intensity of non-linear simulation is less than the intensity of linear simulation :

\(I_{non \, linear} = 114.3 \, kA \)
\(I_{linear} = 133.8 \, kA \)
\(\frac{I_{non \, linear}}{I_{linear}} = 0.854 \, A\)

12.3. Resistance \(R\)

Resistance \(R (Ohm)\)

We can represent this algorithm by diagram :

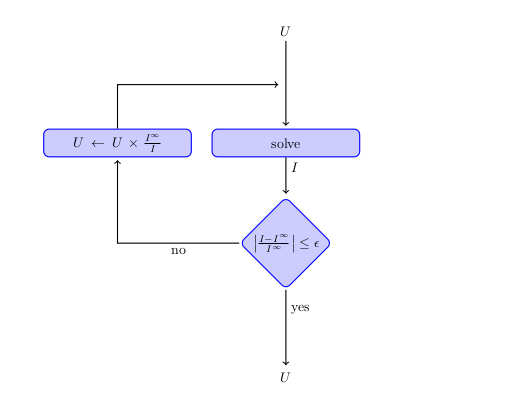
"Diagram of search of Tensions

We can see, the resitance of non-linear simulation is great than the resistance of linear simulation :

\(R_{non \, linear} = 3.50 picoOhm\)
\(R_{linear} = 2.99 picoOhm\)
\(\frac{R_{non \, linear}}{R_{linear}} = 1.171\)

\(\left(\frac{R_{non \, linear}}{R_{linear}} \right)^{-1} = 0.853938785234262\), it’s the ratio of intensity. It’s normal : The Ohm law \(\ U = R \, I\) gives :

\[\begin{eqnarray*} \frac{U}{U} = \frac{R_{non \, linear} \, I_{non \, linear}}{R_{linear} \, I_{linear}} \\ \left(\frac{R_{non \, linear}}{R_{linear}} \right)^{-1} = \frac{I_{non \, linear}}{I_{linear}} \end{eqnarray*}\]

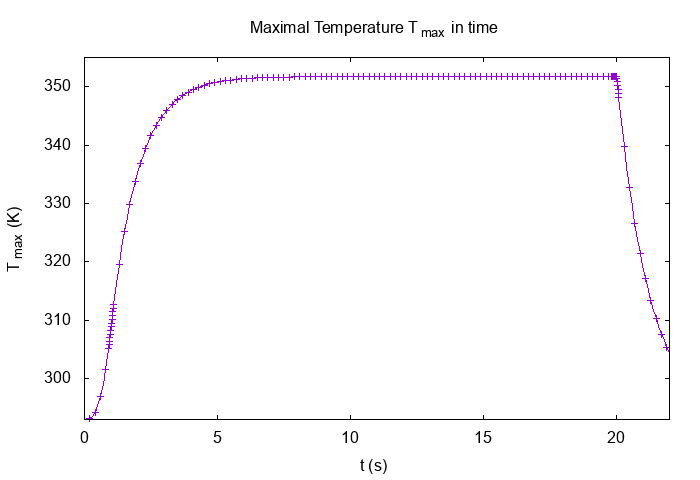
12.4. Temperature \(T\)

Temperature \(\mathbf{T} (K)\) on Or axis

Maximal Temperature \(T_{max} (K)\)

We can see, the temperature of non-linear simulation is less than the temperature of linear simulation :

\(T_{max \, non \, linear} = 351.7 \, K\)
\(T_{max \, linear} = 362.2 \, K\)
\(\frac{T_{max \, non \, linear}}{T_{max \, linear}} = 0.971\)

12.5. Interpretation

On simulation, the temperature increases, thus the resistance (or resistivity) increases, thus the intensity (by Ohm law) and magnetic field is less than the linear case.

Moreover, if the intensity is less, the energy released by Joule’s effect is less. And, the thermal conductivity increases. This two phenomenas give that the temperature of non-linear case is less than linear case.

A non-linear matter is more resistive, thus give less intensity for same tension, but it releases less heat for the same tension.

If you want see the difference between linear and non-linear simulation with same current see Axisymmetrical Case : Interpretation