Test Case of Static Elasticity in Cartesian Coordinates

1. Introduction

This page present a test case to validate the implementation of elastic equation with Hooke law without thermal dilatation in static and cartesian case in vectorial form.

The result permit, or not, to verify if our method for static elasticity resolution is good.

We inject a function, here \(\mathbf{u} = \begin{pmatrix} 0 \\ cos(2\pi \frac{x}{L}) \\ 0 \end{pmatrix}\), we inject in equation (Static Elasticity), we recuperate the associated coefficient. We run a simulation with those coefficient and compare the numeric result with the begining function.

2. Run the calculation

The command line to run this case is :

    mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=elastic.cfg

3. Data Files

The case data files are available in Github here :

CFG file - Edit the file
JSON file - Edit the file
GEO file - Edit the file
SH file - Edit the file : it serves to compute the same test case but with different mesh sizes.

4. Equation

We solve the elastic equation with Hooke law in static and cartesian case (for more detail see section In General Case).

The differential formulation is :

Differential Formulation of Elasticity Equation in Stationary Case

\[\text{(Static Elasticity)} \left\{ \begin{matrix} - \nabla \cdot \bar{\bar{\sigma}} = \mathbf{F} & \text{on } \Omega_c & \text{(Static Elas-1)} \\ \mathbf{u} = \mathbf{u_0} & \text{on } \Gamma_{D \hspace{0.05cm} elas} & \text{(D elas)} \\ \bar{\bar{\sigma}} \cdot \mathbf{n} = g_N & \text{on } \Gamma_{N \hspace{0.05cm} elas} & \text{(N elas)} \\ \bar{\bar{\sigma}} \cdot \mathbf{n} + k \, \mathbf{u} = g_R & \text{on } \Gamma_{R \hspace{0.05cm} elas} & \text{(R elas)} \end{matrix} \right.\]

With :

Lamé’s coefficients : \( \lambda = \frac{E \, \nu}{(1-2 v) \, (1+\nu)}\) and \(\mu = \frac{E}{2 \, (1+\nu)} \) with :
- Young modulus \(E\)
- Poisson’s coefficient \(\nu\)
Displacement \(\mathbf{u} = \begin{pmatrix} u_x \\ u_y \\ u_z \end{pmatrix}\)
tensor of small deformations : \(\bar{\bar{\epsilon}}_{ij} = \frac{1}{2} \left( \nabla \mathbf{u} + \nabla \mathbf{u}^T \right)\)
Stress Tensor : \(\bar{\bar{\sigma}} = \lambda \, Tr(\bar{\bar{\epsilon}}) \, Id + 2 \, \mu \, \bar{\bar{\epsilon}}\)
Stiffness tensor : \(k\)
Volumic Forces : \(\mathbf{F}\)

And notations :

Divergence of tensor : \(\nabla \cdot \bar{\bar{\sigma}} = \begin{pmatrix} \nabla \cdot \bar{\bar{\sigma}}_{x,:} \\ \nabla \cdot \bar{\bar{\sigma}}_{y,:} \\ \nabla \cdot \bar{\bar{\sigma}}_{z,:} \end{pmatrix} = \begin{pmatrix} \frac{\partial \bar{\bar{\sigma}}_{xx}}{\partial x} + \frac{\partial \bar{\bar{\sigma}}_{xy}}{\partial y} + \frac{\partial \bar{\bar{\sigma}}_{xz}}{\partial z} \\ \frac{\partial \bar{\bar{\sigma}}_{yx}}{\partial x} + \frac{\partial \bar{\bar{\sigma}}_{yy}}{\partial y} + \frac{\partial \bar{\bar{\sigma}}_{yz}}{\partial z} \\ \frac{\partial \bar{\bar{\sigma}}_{zx}}{\partial x} + \frac{\partial \bar{\bar{\sigma}}_{zy}}{\partial y} + \frac{\partial \bar{\bar{\sigma}}_{zz}}{\partial z} \end{pmatrix}\)
Scalar produce of tensor : \(\bar{\bar{\sigma}} \cdot \mathbf{n} = \begin{pmatrix} \bar{\bar{\sigma}}_{x,:} \cdot \mathbf{n} \\ \bar{\bar{\sigma}}_{y,:} \cdot \mathbf{n} \\ \bar{\bar{\sigma}}_{z,:} \cdot \mathbf{n} \end{pmatrix} = \begin{pmatrix} \bar{\bar{\sigma}}_{xx} \, n_x + \bar{\bar{\sigma}}_{xy} \, n_y + \bar{\bar{\sigma}}_{xz} \, n_z \\ \bar{\bar{\sigma}}_{yx} \, n_x + \bar{\bar{\sigma}}_{yy} \, n_y + \bar{\bar{\sigma}}_{yz} \, n_z \\ \bar{\bar{\sigma}}_{zx} \, n_x + \bar{\bar{\sigma}}_{zy} \, n_y + \bar{\bar{\sigma}}_{zz} \, n_z \end{pmatrix}\)

5. Geometry

The geometry is a beam.

The geometrical domains are :

Omega : the beam
- Left : left surface
- Right : right surface
- Front : front surface
- Upper : upper surface
- Backward : backward surface
- Bottom : bottom surface

Symbol

Description

value

unit

\(L\)

length of beam

\(10\)

\(w\)

width and height of beam

\(0.3\)

We have \(\Gamma_{D \hspace{0.05cm} elas} = \texttt{Upper} + \texttt{Bottom} + \texttt{Front} + \texttt{Backward}\) and \(\Gamma_{N \hspace{0.05cm} elas} = \texttt{Right} + \texttt{Left}\)

6. Boundary Conditions

We impose the boundary conditions :

Strong Dirichlet on Upper, Bottom, Front and Backward : \(\mathbf{u} = \begin{pmatrix} 0 \\ cos(2\pi \frac{x}{L}) \\ 0 \end{pmatrix}\)
Neumann on Right and Left : \( \bar{\bar{\sigma}} \cdot \mathbf{n} = 0 \)

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file

    "BoundaryConditions":
    {
        "elastic":
        {
            "Dirichlet":
            {
                "Upper":
                {
                    "expr":"{0,cos(2*pi*x/L),0}:x:L"
                },
                "Bottom":
                {
                    "expr":"{0,cos(2*pi*x/L),0}:x:L"
                },
                "Front":
                {
                    "expr":"{0,cos(2*pi*x/L),0}:x:L"
                },
                "Backward":
                {
                    "expr":"{0,cos(2*pi*x/L),0}:x:L"
                }
            },
            "Neumann":
            {
                "Right":
                {
                    "expr":0
                },
                "Left":
                {
                    "expr":0
                }
            }
        }
    }

7. Weak Formulation

We obtain :

Weak Formulation of Elasticity Equation in Stationnary Case

\[\text{(Weak Static Elasticity)} \\ \left\{ \begin{matrix} \int_{\Omega_c}{ \bar{\bar{\sigma}}_{xx} \, \frac{\partial \xi_x}{\partial x} + \bar{\bar{\sigma}}_{xy} \, \frac{\partial \xi_x}{\partial y} + \bar{\bar{\sigma}}_{xz} \, \frac{\partial \xi_x}{\partial z} } \bar{\bar{\sigma}}_{yx} \, \frac{\partial \xi_y}{\partial x} + \bar{\bar{\sigma}}_{yy} \, \frac{\partial \xi_y}{\partial y} + \bar{\bar{\sigma}}_{yz} \, \frac{\partial \xi_y}{\partial z} \bar{\bar{\sigma}}_{zx} \, \frac{\partial \xi_z}{\partial x} + \bar{\bar{\sigma}}_{zy} \, \frac{\partial \xi_z}{\partial y} + \bar{\bar{\sigma}}_{zz} \, \frac{\partial \xi_z}{\partial z} = \int_{\Omega_c}{ \mathbf{F} \, \mathbf{ξ} } + \int_{\Gamma_{N \hspace{0.05cm} elas}}{ \mathbf{g_{N}} \, \mathbf{ξ} } + \int_{\Gamma_{R \hspace{0.05cm} elas}}{ \left( \mathbf{g_{R}} - \left( k \, \mathbf{u} \right) \right) \, \mathbf{ξ} } \\ \text{for } \mathbf{ξ} = \begin{pmatrix} \xi_x \\ \xi_y \\ \xi_z \end{pmatrix} \in H^1_{u_0}(\Omega_c) \end{matrix} \right.\]

8. Solution

We take a function \(u = \begin{pmatrix} \frac{e^z}{r} \\ \frac{e^z}{r} \end{pmatrix}\). For Robin condition we put \(k=\begin{pmatrix} \mu & 0 \\ 0 & \mu \end{pmatrix}\). We inject that on (Static Elasticity) and we obtain :

\[\begin{align*} \mathbf{F} &= \begin{pmatrix} 0 \\ \left( \frac{2\pi}{L} \right)^2 \mu cos(2\pi \frac{x}{L}) \\ 0 \end{pmatrix} & \text{ on } \texttt{Omega} \\ g_N &= 0 & \text{ on } \texttt{Right}+\texttt{Left} \\ \end{align*}\]

9. Parameters

The parameters of problem are :

Symbol

Description

Value

Unit

\(E\)

Young modulus

\(2.1e-6\)

\(Pa\)

\(v\)

Poisson’s coefficient

\(0.33\)

\(dimensionless\)

\(\lambda\)

Lamé’s coefficient

\(\frac{E \, v}{(1-2 v) \, (1+v)}\)

\(Pa\)

\(\mu\)

Lamé’s coefficient

\(\frac{E}{2 \, (1+v)}\)

\(Pa\)

\(F = \begin{pmatrix} F_r \\ F_z \end{pmatrix}\)

term source

\(\begin{pmatrix} 0 \\ \left( \frac{2\pi}{L} \right)^2 \mu cos(2\pi \frac{x}{L}) \\ 0 \end{pmatrix}\)

\(N / m^3\)

On JSON file, the parmeters are writed :

Parameters on JSON file

    "Parameters": {
        "E": 1e6,
        "nu": 0.3,
        "mu": "E/(2*(1+nu)):E:nu",
        "lambda":"E*nu/((1+nu)*(1-2*nu)):E:nu",
        "L":10,
        "Fx":"0",
        "Fy":"(2*pi/L)*(2*pi/L)*mu*cos(2*pi*x/L):L:x:mu:lambda",
        "Fz":"0"
    }

10. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficients associate to Weak Formulation are :

Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\mu\)

\(\gamma\)

conservative flux source term

\(\begin{pmatrix} - \lambda \nabla \cdot \mathbf{u} - \mu \frac{\partial u_x}{\partial x} & - \mu \left( \frac{\partial u_y}{\partial x} + \frac{\partial u_x}{\partial y} \right) & - \mu \left( \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z} \right) \\ - \mu \left( \frac{\partial u_y}{\partial x} + \frac{\partial u_x}{\partial y} \right) & - \lambda \nabla \cdot \mathbf{u} - \mu \frac{\partial u_y}{\partial y} & - \mu \left( \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z} \right) \\ - \mu \left( \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z} \right) & - \mu \left( \frac{\partial u_z}{\partial y} + \frac{\partial u_y}{\partial z} \right) & - \lambda \nabla \cdot \mathbf{u} - \mu \frac{\partial u_z}{\partial z} \end{pmatrix}\)

\(f\)

source term

\(\begin{pmatrix} F_x \\ F_y \\ F_z \end{pmatrix}\)

On JSON file, the coefficients are writed :

CFPDEs coefficients on JSON file

    "Materials":
    {
        "Omega":
        {
            "elastic_c": "mu:mu",
            "elastic_gamma":"{-lambda*(elastic_div_u) - mu*elastic_grad_u_00,-mu*elastic_grad_u_10,-mu*elastic_grad_u_20, -mu*elastic_grad_u_01,-lambda*(elastic_div_u) - mu*elastic_grad_u_11,-mu*elastic_grad_u_21, -mu*elastic_grad_u_02,-mu*elastic_grad_u_12,-lambda*(elastic_div_u) - mu*elastic_grad_u_22}:lambda:mu:elastic_div_u:elastic_grad_u_00:elastic_grad_u_01:elastic_grad_u_10:elastic_grad_u_11:elastic_grad_u_20:elastic_grad_u_21:elastic_grad_u_22:elastic_grad_u_02:elastic_grad_u_12",
            "elastic_f": "{Fx,Fy,Fz}:Fx:Fy:Fz"
        }
    }

11. Validation

We compute the L2-error between numerical solution and begining function with different size of mesh :

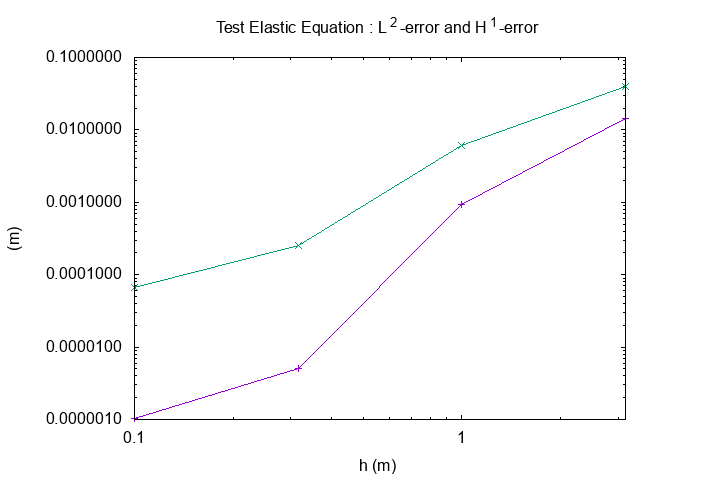
\(L^2-error\)

The method converge with polynomial order, the L2-error form a right in xy logarithmic scale.

Conclusion : We trust on this method to solve the static elasticity equation (Static Elasticity).