Test Case of Elasto-Magnetism in Stationary and Axisymmetrical Case

1. Introduction

This page presents the simulation and result of page Elastic Equations with Electromagnetism and Thermic in Axisymmetrical case : Elastic and Electromagnetism problem coupled by Laplace Force in stationnary and axisymmetrical case.

2. Run the calculation

The command line to run this case is :

    mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=elasto-thermo-mag.cfg --cfpdes.gmsh.hsize=5e-3

To compute with only the Laplace Force, please, put :

        "bool_laplace":1,
        "bool_dilatation":0,

On Parameter function of .json file elasto-thermo-mag.json.

3. Data Files

The case data files are available in Github here :

CFG file - Edit the file
JSON file - Edit the file
GEO file - Edit the file

4. Equation

In this subsection, we couple the equation (Static Elasticity Axis) of Elastic equation and (AV Axis) AV-Formulation in axisymmetrical coordinates.

The domain of resolution of electromagnetism part is \(\Omega^{axis}\) with bounds \(\Gamma^{axis}\), \(\Gamma_D^{axis}\) the bound of Dirichlet conditions and \(\Gamma_N^{axis}\) the bound of Neumann conditions such that \(\Gamma^{axis} = \Gamma_N^{axis} \cup \Gamma_D^{axis}\).

The domain of resolution of elastic part is \(\Omega_c^{axis} \subset \Omega^{axis}\) (and the domain of definition of electrical potential \(V\) and electrical conductivity \(\sigma\)) with bounds \(\Gamma_c^{axis}\), \(\Gamma_{D \hspace{0.05cm} elas}^{axis}\) the bound of Dirichlet conditions and \(\Gamma_{N \hspace{0.05cm} elas}^{axis}\) the bound of Neumann conditions such that \(\Gamma_c^{axis} = \Gamma_{D \hspace{0.05cm} elas}^{axis} \cup \Gamma_{N \hspace{0.05cm} elas}^{axis}\). The domain \(\Omega_c^{axis}\) correspond to the conductor.

Differential Formulation of Elastic Thermic Electromagnetism Equations

\[\small{ \text{(Elasto-Thermo-Elec)} \\ \left\{ \begin{align*} \nabla \times \left( \frac{1}{\mu} \nabla \times \textbf{A} \right) + \sigma(T) \frac{\partial \textbf{A}}{\partial t} + \sigma(T) \nabla V &= 0 & \text{ on } \Omega & \text{(AV-1)} \\ \nabla \cdot \left( \sigma(T) \nabla V + \sigma(T) \frac{\partial \textbf{A}}{\partial t} \right) &= 0 & \text{ on } \Omega_c & \text{(AV-2)} \\ \rho C_p \, \frac{\partial T}{\partial t} - k(T) \Delta T &= \sigma(T) \left( \nabla V + \frac{\partial \mathbf{A}}{\partial t} \right) \cdot \left( \nabla V + \frac{\partial \mathbf{A}}{\partial t} \right) & \text{ on } \Omega_c & \text{(Heat-1)} \\ \frac{\partial \mathbf{p}}{\partial t} - \nabla \cdot \bar{\bar{\sigma}} &= \sigma(T) \, \left( - \nabla V - \frac{d \mathbf{A}}{dt} \right) \times \left( \nabla \times \mathbf{A} \right) & \text{on } \Omega_c & \text{(Elas-1)} \\ \mathbf{A} \times \mathbf{n} &= 0 & \text{ on } \Gamma_D & \text{(AV-D)} \\ \left( \nabla \times \mathbf{A} \right) \times \mathbf{n} &= 0 & \text{ on } \Gamma_N & \text{(AV-N)} \\ \frac{\partial T}{\partial \mathbf{n}} &= 0 & \text{ on } \Gamma_{Nc} & \text{(Heat-N)} \\ - k(T) \, \frac{\partial T}{\partial \mathbf{n}} &= h \, \left( T - T_c \right) & \text{ on } \Gamma_{Rc} & \text{(Heat-R)} \\ \mathbf{u} &= \mathbf{u_0} & \text{on } \Gamma_{D \hspace{0.05cm} elas} & \text{(Elas-D)} \\ \bar{\bar{\sigma}} \cdot \mathbf{n} &= g_N & \text{on } \Gamma_{N \hspace{0.05cm} elas} & \text{(Elas-N)} \\ \end{align*} \right. }\]

With :

Magnetic Potential Field \(\mathbf{A}\)

Temperature \(T\)

Electrical Potential Scalar \(V\)

Thermal Conductivity \(k(T)=\frac{k_0}{1+\alpha (T-T_0)} \frac{T}{T_0}\)

Electrical Conductivity \(\sigma(T)=\frac{\sigma_0}{1+\alpha (T-T_0)}\)

Density \(\rho\)

Thermal Capacity \(C_p\)

Cooling Temperature \(T_c\)

Reference Temperature \(T_0\)

Displacement \(\mathbf{u}\)

Momentum \(\mathbf{p} = \frac{\partial \left( \rho \, \mathbf{u} \right)}{\partial t}\)

Stress Tensor \(\bar{\bar{\sigma}}(\bar{\bar{\epsilon}}) = \bar{\bar{\sigma}}^E(\bar{\bar{\epsilon}})\)

The tensor of small deformations \(\bar{\bar{\epsilon}} = \frac{1}{2} \left( \nabla \mathbf{u} + \nabla \mathbf{u}^T \right)\)

Lamé’s coefficients : \(\lambda = \frac{E \, v}{(1-2 v) \, (1+v)}\), \(\mu = \frac{E}{2 \, (1+v)}\) with the Young modulus \(E\) and Poisson’s coefficient \(v\)

The equation become coupled in one senses, the second equation (Elas-1 Axis) depends of potentials.

We don’t care of geometrical deformation which can change the mesh or the density. We suppose the geometry is fixed.

5. Geometry

The geometry is a torus of the conductor in cartesian coordinates \((x,y,z)\) or rectangle in axisymmetric coordinates \((r,z)\), surrounded by air.

Geometry in axisymmetrical cut loop on Conductor

Geometry in axisymmetrical cut

Geometry in three dimensions

Geometry in three dimensions cut loop on Conductor

The geometrical domains are :

Conductor : the torus is composed by conductor material
- Interior : interior surface of conductor ring
- Exterior : exterior surface of conductor ring
- Upper : upper of conductor ring
- Bottom : bottom of conductor ring
Air : the air surround Conductor
- zAxis : a bound of Air, correspond to \(Oz\) axis (\(\{(z,r), \, z=0 \}\))
- infty : the rest of bound of Air

Symbol

Description

value

unit

\(r_{int}\)

interior radius of torus

\(75e-3\)

\(r_{ext}\)

exterior radius of torus

\(100.2e-3\)

\(z_1\)

half-height of torus

\(300e-3\)

\(r_{infty}\)

radius of infty border

\(5*r_{ext}\)

6. Boundary Conditions

We impose the boundary conditions :

For Electrical equation of unknow electric potential \(V\) :
- On V0 : \(V = 0\)
- On V1 : \(V = \frac{1}{4} \left\{ \begin{matrix} t \text{ on } 0s \leq t < 1s \\ 1 \text{ on } 1s \leq t < 20s \\ t \text{ on } 20s \leq t \end{matrix} \right.\)
For Magnetic equation of unknow magnetic potential field \(\mathbf{A}\) :
- On OXOZ and V0 : \(A_x = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OXOZ and V0
- On OYOZ and V1 : \(A_y = A_z = 0\), we want \(\mathbf{A}\) orthogonal to OYOZ and V1
- Infty : We approximate the problem, Infty is the physical infty thus \(\mathbf{B}=0\) at Infty thus \(\mathbf{A} = 0\).
For Heat equation of unknow \(T\) :
- On V0, V1, Upper and Bottom, we put Neumann condition \(\frac{\partial T}{\partial \mathbf{n}} = 0\)
- On Interior and Exterior, we put Robin condition \(k \frac{\partial T}{\partial \mathbf{n}} = h \, \left( T - T_c \right)\). It represents the cooling by water.
For Elastic equation of unknow displacement \(u\) :
- On Upper and Bottom, we put Strong Dirichlet condition : \(\mathbf{u} = 0\). The Dirichlet condition represents the embedding of mechanical part.
- On Interior and Exterior, we put Neumann condition : \(\bar{\bar{\sigma}} \cdot \mathbf{n} = 0\). The Neumann condition represents the freedom of displacement.
- On V_0, we put Component Strong Dirichlet : \(u_y = 0\).
- On V_1, we put Component Strong Dirichlet : \(u_x = 0\).

The two Component Strong Dirichlet for Elastic equation represents the fact that the quart of torus is the simplification of a complete torus and because the problem is axisymmetric, the displacement must be on \(O_{rz}\) plan (here it’s \(O_{xz}\) for V0 and \(O_{yz}\) for V1).

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file

    "BoundaryConditions":
    {
        "magnetic":
        {
            "Dirichlet":
            {
                "magdir":
                {
                    "markers":["ZAxis","Infty"],
                    "expr":"0"
                }
            }
        },
        "heat":
        {
            "Robin":
            {
                "heatdir":
                {
                    "markers":["Interior","Exterior"],
                    "expr1":"h*x:h:x",
                    "expr2":"h*T_c*x:h:T_c:x"
                }
            }
        },
        "elastic":
        {
            "Dirichlet":
            {
                "elasdir":
                {
                    "markers":["Upper","Bottom"],
                    "expr":"{0,0}"
                }
            }
        }
    }

7. Weak Formulation

We obtain :

Weak Formulation of Elastic Thermic Electromagnetism Equations in Stationnary Case Vectorial

\[\tiny{ \text{(Weak Elas-Heat-AV Static)} \\ \begin{eqnarray*} \int_{\Omega}{\frac{1}{\mu} (\nabla \times \textbf{A}) \cdot (\nabla \times \mathbf{ϕ})} + \int_{\Omega_c}{ \sigma \nabla V \cdot \mathbf{ϕ} } + \int_{\Omega}{ \sigma \frac{d \mathbf{A}}{d t} \cdot \mathbf{ϕ} } &=& 0 &\text{(Weak AV-1)} \\ \int_{\Omega_c}{\sigma (\nabla V + \frac{d \mathbf{A}}{d t}) \cdot \nabla \mathbf{\psi}} &=& 0 & \text{(Weak AV-2)} \\ \int_{\Omega_c}{ k \, \nabla T \cdot \nabla \eta } + \int_{\Gamma_R}{ h \, T \, \eta } &=& \int_{\Omega_c}{ Q \, \eta } + \int_{\Gamma_R}{ h \, T_c \, \eta } & \text{(Weak Heat Axis)} \\ \int_{\Omega_c}{ \bar{\bar{\sigma}}_{xx} \, \frac{\partial \xi_x}{\partial x} + \bar{\bar{\sigma}}_{xy} \, \frac{\partial \xi_x}{\partial y} + \bar{\bar{\sigma}}_{xz} \, \frac{\partial \xi_x}{\partial z} + \bar{\bar{\sigma}}_{yx} \, \frac{\partial \xi_y}{\partial x} + \bar{\bar{\sigma}}_{yy} \, \frac{\partial \xi_y}{\partial y} + \bar{\bar{\sigma}}_{yz} \, \frac{\partial \xi_y}{\partial z} + \bar{\bar{\sigma}}_{zx} \, \frac{\partial \xi_z}{\partial x} + \bar{\bar{\sigma}}_{zy} \, \frac{\partial \xi_z}{\partial y} + \bar{\bar{\sigma}}_{zz} \, \frac{\partial \xi_z}{\partial z} } &=& \int_{\Omega_c}{ \mathbf{F}_{laplace} \cdot \mathbf{ξ} } + \int_{\Gamma_{N \hspace{0.05cm} elas}}{ \mathbf{g_N} \cdot \mathbf{ξ} } + \int_{\Gamma_{R \hspace{0.05cm} elas}}{ \left( \mathbf{g_R} - ku \right) \cdot \mathbf{ξ} } & \text{(Weak Elas)} \\ \text{for } \mathbf{ϕ} \in H^1(\Omega)^2, \ \psi \in H^1(\Omega_c) , \ \eta \in H^1(\Omega_c) \ \xi = \begin{pmatrix} \xi_x \\ \xi_y \\ \xi_z \end{pmatrix} \in H^1(\Omega_c)^2 \ && \text{and} \ \mathbf{F}_{laplace} = \begin{pmatrix} F_{laplace \, x} \\ F_{laplace \, y} \\ F_{laplace \, z} \end{pmatrix} = - \sigma \, \nabla V \times \left( \nabla \times \mathbf{A} \right) \end{eqnarray*} }\]

8. Parameters

The parameters of problem are :

On Conductor :

Symbol

Description

Value

Unit

\(V_0\)

scalar electrical potential on V0

\(0\)

\(Volt\)

\(V_1\)

scalar electrical potential on V0

\(\frac{1}{4} \times 0.2\)

\(Volt\)

\(\sigma\)

electrical conductivity

\(58e6\)

\(S/m\)

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg.m/A^2/S^2\)

\(k\)

thermal conductivity

\(380\)

\(W/m/K\)

\(C_p\)

thermal capacity

\(380\)

\(J/K/kg\)

\(\rho\)

density

\(10000\)

\(kg/m^3\)

\(h\)

convective coefficient

\(80000\)

\(W/m^2/K\)

\(T_c\)

cooling temperature

\(293\)

\(K\)

\(T_0\)

temperature of reference or rest temperature

\(293\)

\(K\)

\(E\)

Young Modulus

\(2.1e6\)

\(Pa\)

\(\nu\)

Poisson’s coefficient

\(0.33\)

\(dimensionless\)

\(Lame\_\lambda\)

Lame’s coefficient

\(\frac{E \, v}{(1-2v)(1+v)}\)

\(Pa\)

\(Lame\_\mu\)

Lame’s coefficient

\(\frac{E}{2 (1+v)}\)

\(Pa\)

\(\alpha_T\)

linear coefficient of dilatation

\(17e-6\)

\(K^{-1}\)

\(\sigma_T = -\frac{E}{1-2*nu} alpha_T (T-T0)\)

thermal dilatation term

\(\frac{E}{2 (1+v)}\)

\(Pa\)

On Air :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

On JSON file, the parmeters are writed :

Parameters on JSON file

    "Parameters":
    {
        "bool_laplace":1,
        "bool_dilatation":0,

        "h":80000,      // W/m2/K
        "T_c":293,      // K
        "T0":293,       // K

        // Constants of analytical solve
        "a":77.32,      // K
        "b":0.40041,    // K
        "rmax":0.0861910719118454,  // m
        "Tmax":295.85   // K
    }

9. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficient associate to Weak Formulation are :

For MQS equation (Weak MQS Axis) :
- On Conductor :
Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\frac{1}{\mu}\)

\(f\)

source term

\(- \sigma \, \nabla V\)
- On Air :
Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(\frac{1}{\mu}\)
For heat equation, on Conductor (the temperature isn’t computed on Air)

Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(k\)

\(f\)

source term

\(\sigma \Vert \nabla V \Vert\)

For elastic equation, on Conductor (the displacement isn’t computed on Air) :

Coefficient

Description

Expression

\(c\)

diffusion coefficient

\(Lame\_\mu\)

\(\gamma\)

conservative flux source term

\(\begin{pmatrix} - Lame\_\lambda \nabla \cdot \mathbf{u} - Lame\_\mu \frac{\partial u_x}{\partial x} & -Lame\_\mu \frac{\partial u_y}{\partial x} & -Lame\_\mu \frac{\partial u_z}{\partial x} \\ -Lame\_\mu \frac{\partial u_x}{\partial y} & - Lame\_\lambda \nabla \cdot \mathbf{u} - Lame\_\mu \frac{\partial u_y}{\partial y} & -Lame\_\mu \frac{\partial u_z}{\partial y} \\ -Lame\_\mu \frac{\partial u_x}{\partial z} & -Lame\_\mu \frac{\partial u_y}{\partial z} & - Lame\_\lambda \nabla \cdot \mathbf{u} - Lame\_\mu \frac{\partial u_z}{\partial z} \end{pmatrix}\)

\(f\)

source term

\(\mathbf{F_{laplace}} = \begin{pmatrix} \frac{\partial V}{\partial y} \left( \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right) + \frac{\partial V}{\partial z} \left( - \frac{\partial A_z}{\partial y} + \frac{\partial A_y}{\partial z} \right) \\ \frac{\partial V}{\partial x} \left( \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right) - \frac{\partial V}{\partial z} \left( - \frac{\partial A_z}{\partial y} + \frac{\partial A_y}{\partial z} \right) \\ \frac{\partial V}{\partial x} \left( -\frac{\partial A_z}{\partial x} + \frac{\partial A_x}{\partial z} \right) + \frac{\partial V}{\partial y} \left( \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z} \right) \end{pmatrix}\)

On JSON file, the coefficients are writed :

CFPDEs coefficients on JSON file

   "Materials":
    {
        "Conductor":
        {
            // Magnetic Part
            "U":0.2,            // Volt
            "sigma":58e+6,      // S.m-1
            "mu":"4*pi*1e-7",   // kg.m/A2/S2

            "j_th":"-sigma*U/2/pi/x:sigma:U:x",

            "magnetic_c":"x/mu:x:mu",
            "magnetic_beta":"{2/mu,0}:mu",
            "magnetic_f":"-sigma*U/2/pi*x:sigma:U:x",

            // Heat Part
            "k":380,            // W/m/K
            "heat_c":"k*x:k:x",
            "heat_f":"sigma*U/(2*pi)*U/(2*pi)/x:sigma:U:x",

            // Elastic Part
            "E":2.1e6,          // Pa
            "v":0.33,           // dimensionless
            "alpha_T":"17e-6",  // K-1

            "Lame_lambda":"E*v/(1-2*v)/(1+v):E:v",
            "Lame_mu":"E/(2*(1+v)):E:v",

            "F_laplace":"{1/x*j_th*magnetic_grad_phi_0, 1/x*j_th*magnetic_grad_phi_1}::x:j_th:magnetic_grad_phi_0:magnetic_grad_phi_0:magnetic_grad_phi_1",
            "sigma_T":"-(3*Lame_lambda+2*Lame_mu)*alpha_T*(heat_T-T0):Lame_lambda:Lame_mu:alpha_T:heat_T:T0",

            "elastic_c":"x*Lame_mu:x:Lame_mu",
            "elastic_gamma":"{-Lame_lambda*(x*elastic_grad_u_00+elastic_u_0+x*elastic_grad_u_11)-x*Lame_mu*elastic_grad_u_00-bool_dilatation*x*sigma_T, -x*Lame_mu*elastic_grad_u_10, -x*Lame_mu*elastic_grad_u_01, -Lame_lambda*(x*elastic_grad_u_00+elastic_u_0+x*elastic_grad_u_11)-x*Lame_mu*elastic_grad_u_11-bool_dilatation*x*sigma_T}:bool_dilatation:x:Lame_lambda:Lame_mu:elastic_u_0:elastic_grad_u_00:elastic_grad_u_01:elastic_grad_u_10:elastic_grad_u_11:sigma_T",
            "elastic_f":"{bool_laplace*x*F_laplace_0-Lame_lambda*elastic_grad_u_00-(Lame_lambda+2*Lame_mu)*elastic_u_0/x-Lame_lambda*elastic_grad_u_11-bool_dilatation*sigma_T, bool_laplace*x*F_laplace_1}:bool_laplace:bool_dilatation:x:F_laplace_0:F_laplace_1:Lame_mu:Lame_lambda:elastic_u_0:elastic_grad_u_00:elastic_grad_u_01:elastic_grad_u_11:sigma_T",

            "sigma_rr":"(Lame_lambda+2*Lame_mu)*elastic_grad_u_00+Lame_lambda*elastic_u_0/x+Lame_lambda*elastic_grad_u_11+bool_dilatation*sigma_T:bool_dilatation:Lame_lambda:Lame_mu:x:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:elastic_grad_u_22:sigma_T",
            "sigma_thth":"Lame_lambda*elastic_grad_u_00+(Lame_lambda+2*Lame_mu)*Lame_lambda*elastic_u_0/x+Lame_lambda*elastic_grad_u_11+bool_dilatation*sigma_T:bool_dilatation:Lame_lambda:Lame_mu:x:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:elastic_grad_u_22:sigma_T",
            "sigma_zz":"Lame_lambda*elastic_grad_u_00+Lame_lambda*Lame_lambda*elastic_u_0/x+(Lame_lambda+2*Lame_mu)*elastic_grad_u_11+bool_dilatation*sigma_T:bool_dilatation:Lame_lambda:Lame_mu:x:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:elastic_grad_u_22:sigma_T",
            "sigma_rz":"Lame_mu*(elastic_grad_u_01+elastic_grad_u_10):Lame_mu:elastic_grad_u_01:elastic_grad_u_10",

            "sigma_1":"Lame_lambda/x*elastic_u_0+(Lame_lambda+Lame_mu)*(elastic_grad_u_00+elastic_grad_u_11)+bool_dilatation*sigma_T+Lame_mu*sqrt((elastic_grad_u_00-elastic_grad_u_11)*(elastic_grad_u_00-elastic_grad_u_11)+4*(elastic_grad_u_01+elastic_grad_u_10)*(elastic_grad_u_01+elastic_grad_u_10)):bool_dilatation:x:Lame_lambda:Lame_mu:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:elastic_grad_u_01:elastic_grad_u_10:sigma_T",
            "sigma_2":"Lame_lambda*elastic_grad_u_00+(Lame_lambda+2*Lame_mu)/x*elastic_u_0+Lame_lambda*elastic_grad_u_11+bool_dilatation*sigma_T:bool_dilatation:x:Lame_lambda:Lame_mu:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:sigma_T",
            "sigma_3":"Lame_lambda/x*elastic_u_0+(Lame_lambda+Lame_mu)*(elastic_grad_u_00+elastic_grad_u_11)+bool_dilatation*sigma_T-Lame_mu*sqrt((elastic_grad_u_00-elastic_grad_u_11)*(elastic_grad_u_00-elastic_grad_u_11)+4*(elastic_grad_u_01+elastic_grad_u_10)*(elastic_grad_u_01+elastic_grad_u_10)):bool_dilatation:x:Lame_lambda:Lame_mu:elastic_u_0:elastic_grad_u_00:elastic_grad_u_11:elastic_grad_u_01:elastic_grad_u_10:sigma_T"
        },
        "Air":
        {
            "physics":"magnetic",
            "mu":"4*pi*1e-7",   // kg.m/A2/s2
            "magnetic_c":"x/mu:x:mu",
            "magnetic_beta":"{2/mu,0}:mu"
        }
    }

10. Numeric Parameters

Mesh size :
- Interior of torus : \(0.01 m\)
- Far from the torus : \(0.2 m\)
Element Type : I run the simulation in \(P_2\) elements.

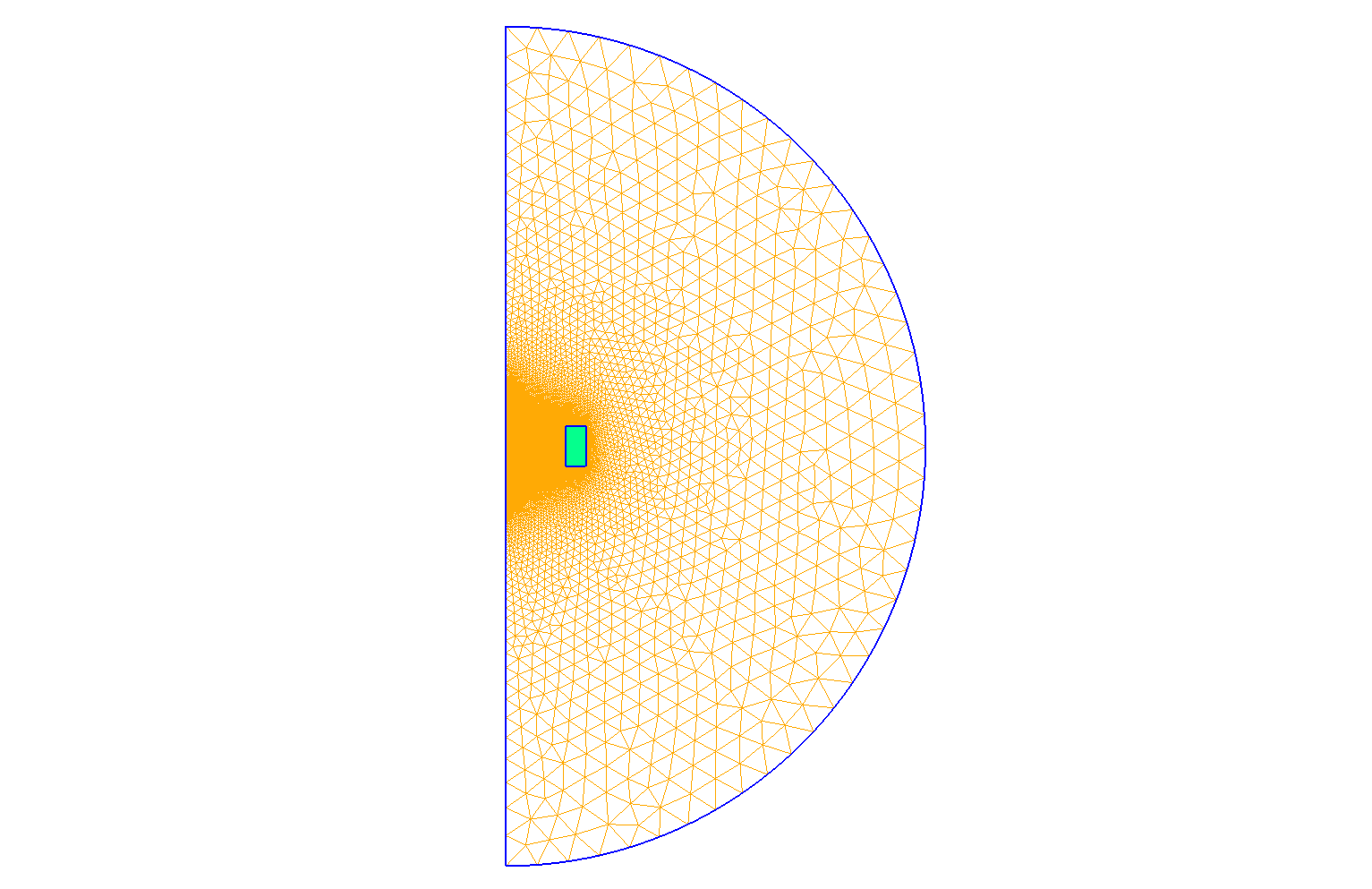
Mesh of Geometry

11. Exact solutions

11.1. Displacement on Or axis

The calculus is based on book Solenoid Magnet Design but it presents an error.

11.1.1. Approximations

We want to compute exactly the displacement on \(r=0\), for that, we suppose that the height is infinitely great. The elastic equations is reduced in its r-component :

\[ - \bar{\bar{\sigma}}_{\theta \theta} + \frac{\partial \left( r \bar{\bar{\sigma}}_{rr} \right)}{\partial r} = - r \, J_{\theta} \, B_z\]

The z component of displacement is null : \(u_z = 0\).

And the stress tensor :

\[\begin{eqnarray*} \bar{\bar{\sigma}}_{rr} &=& \frac{E}{(1-2 v)(1+v)} \left( (1-v) \frac{\partial u_r}{\partial r} + v \frac{u_r}{r} \right) \\ \bar{\bar{\sigma}}_{\theta \theta} &=& \frac{E}{(1-2 v)(1+v)} \left( v \frac{\partial u_r}{\partial r} + (1-v) \frac{u_r}{r} \right) \end{eqnarray*}\]

And \(\sigma_{zz} = \sigma_{rz} = 0\).

Thus, the elastic equation is writed :

\[ \frac{\partial}{\partial r} \left( r \frac{\partial u_r}{\partial r} \right) - \frac{u_r}{r} = - \frac{(1+v)(1-2v)}{E (1-v)} \, r \, J_{\theta} \, B_z\]

The solve \(u_r\) can be write in this form :

\[ u_r(r) = C_1 \, r + \frac{C_2}{r} + u_{pr}(r)\]

With \(C_1\), \(C_2\) two constants and \(u_{pr}\) a particular solve.

11.1.2. Compute of \(B_z\)

To compute \(u_{pr}\), we must to compute the magnetic field \(B\).

With the supposition of infinitely height, the r-component \(B_r\) is null \(B_r = 0\) and z-component depend uniquely of r \(B_z=B_z(r)\).

The Ampère Theorem gives us :

\[ \int_{C}{\mathbf{B} \cdot d \mathbf{l}} = \frac{1}{\mu} \, \int_{S}{ \mathbf{J} \cdot \mathbf{n} d S}\]

With \(S\) an any surface and \(C\) its bound.

We take \(S\) a square center in Or axis.

We have :

\[ B_z(r_{int}) - B_z(r) = \frac{1}{\mu} \, \int_{\tau=r_{int}}^{r}{ J_{\theta}(\tau) \, d\tau }\]

The distribution of current density \(J_{\theta}\) of magnet is of the form : \(J_{\theta} = J_{int} \, \frac{r_{int}}{r}\) with \(J_{int} = J_{\theta}(r_{int})\).

For this problem, we have \(J_{\theta} = \frac{U}{2\pi} \, \frac{1}{r}\).

It give :

\[ B_z(r) = B_z(r_{int}) - \frac{\Delta B_z}{ln(r_{ext}/r_{int})} \, ln(\frac{r}{r_{int}})\]

With \(\Delta B_z = B_z(r_{int}) - B_z(r_{ext})\)

11.1.3. Compute of \(u_{pr}\)

\(u_{pr}\) verify :

\[ \frac{\partial }{\partial r} \left( r \frac{\partial u_{pr}}{\partial r} \right) - \frac{u_{pr}}{r} = - \frac{(1+v)(1-2v)}{E (1-v)} \, r \, J_{\theta} \, B_z\]

With current density magnet distribution \(J_{\theta} = J_{int} \, \frac{r_{int}}{r}\) :

\[ \frac{\partial}{\partial r} \left( r \frac{\partial u_{pr}}{\partial r} \right) - \frac{u}{r} = - \frac{(1+v)(1-2v)}{E (1-v)} J_{int} r_{int} \left( \frac{\Delta B_z}{ln(r_{ext}/r_{int})} \, ln(\frac{r}{r_{int}}) \right)\]

It give :

\[ u_{pr}(r) = \frac{(1+v)(1-2v)}{E (1-v)} \, J_{int} r_{int} \, \frac{1}{4} \, r ln(\frac{r}{r_{int}}) \left[ \frac{\Delta Bz}{ln(r_{ext}/r_{int})} \, ln(\frac{r}{r_{int}}) - 2 B_z(r_{int}) + \frac{\Delta B_z}{ln(r_{ext}/r_{int})} \right]\]

Or :

\[ u_{pr}(r) = - \frac{(1+v)(1-2v)}{E (1-v)} \, J_{int} r_{int} \, \frac{1}{4} \, r ln(\frac{r}{r_{int}}) \left[ B_z(r) + B_z(r_{int}) + \frac{\Delta B_z}{ln(r_{ext}/r_{int})} \right]\]

11.1.4. Compute of constants

Nox, we introduce the boundary conditions. We have Neumann condition on \(r=r_{int}\) and \(r=r_{ext}\) :

\[\begin{eqnarray*} \sigma_{rr}(r_{int}) = 0 \\ \sigma_{rr}(r_{ext}) = 0 \end{eqnarray*}\]

With the expression of \(u\) :

\[\begin{eqnarray*} C_1 + (2v-1) \frac{C_2}{r_{int}^2} + (1-v) \frac{\partial u_r(r_{int})}{\partial r} + v \frac{u_r(r_{int})}{r_{int}} &=& 0 \\ C_1 + (2v-1) \frac{C_2}{r_{ext}^2} + (1-v) \frac{\partial u_r(r_{ext})}{\partial r} + v \frac{u_r(r_{ext})}{r_{ext}} &=& 0 \end{eqnarray*}\]

We obtain :

\[\begin{eqnarray*} C_1 &=& \frac{1}{r_{int}^2-r_{ext}^2} \left( r_{ext}^2 \left( (1-v) \frac{\partial u_r}{\partial r}(r_{ext}) + v \frac{u_r(r_{ext})}{r_{ext}} \right) - r_{int}^2 \left( (1-v) \frac{\partial u_r}{\partial r}(r_{int}) + v \frac{u_r(r_{int})}{r_{int}} \right) \right) \\ C_2 &=& \frac{1}{2v-1} \frac{r_{int}^2 r_{ext}^2}{r_{int}^2-r_{ext}^2} \left( (1-v) \frac{\partial u_r}{\partial r}(r_{int}) + v \frac{u_r(r_{int})}{r_{int}} - (1-v) \frac{\partial u_r}{\partial r}(r_{ext}) - v \frac{u_r(r_{ext})}{r_{ext}} \right) \end{eqnarray*}\]

11.1.5. Conclusion

The exact solution of elastic equation for infinitely height is :

\[\left\{ \begin{eqnarray*} u_r(r) &=& C_1 \, r + \frac{C_2}{r} + u_{pr}(r) \\ u_{pr}(r) &=& - \frac{(1+v)(1-2v)}{E (1-v)}\, J_{int} r_{int} \, \frac{1}{4} \, r ln(\frac{r}{r_{int}}) \left[ B_z(r) + B_z(r_{int}) + \frac{\Delta B_z}{ln(r_{ext}/r_{int})} \right] \\ C_1 &=& \frac{1}{r_{int}^2-r_{ext}^2} \left( r_{ext}^2 \left( (1-v) \frac{\partial u_r}{\partial r}(r_{ext}) + v \frac{u_r(r_{ext})}{r_{ext}} \right) - r_{int}^2 \left( (1-v) \frac{\partial u_r}{\partial r}(r_{int}) + v \frac{u_r(r_{int})}{r_{int}} \right) \right) \\ C_2 &=& \frac{1}{2v-1} \frac{r_{int}^2 r_{ext}^2}{r_{int}^2-r_{ext}^2} \left( (1-v) \frac{\partial u_r}{\partial r}(r_{int}) + v \frac{u_r(r_{int})}{r_{int}} - (1-v) \frac{\partial u_r}{\partial r}(r_{ext}) - v \frac{u_r(r_{ext})}{r_{ext}} \right) \end{eqnarray*} \right.\]