Test case of Transient Heat Equation in Axisymmetric

1. Introduction

This page presents the simulation of temperature on geometry of torus in transient case and axisymmetrical case with electric source term computed with CFPDEs application.

The electric source term isn’t the real physics source term because it varies over time.

2. Run the calculation

The command line to run this case is :

    mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=heat.cfg --cfpdes.gmsh.hsize=1e-4

3. Data Files

The case data files are available in Github here :

4. Equation

We solve the Heat Equation in Axisymmetrical coordinates (Heat Axis).

Heat equation in axisymmetric coordinates
\[\text{(Heat Axis)} \left\{ \begin{matrix} \rho C_p \, \frac{\partial T}{\partial t} - k \Delta T = Q \text{ on } \Omega_c^{axis} \\ \frac{\partial T}{\partial \mathbf{n}^{axis}} = 0 \text{ on } \Gamma_N^{axis} \\ - k \, \frac{\partial T}{\partial \mathbf{n}^{axis}} = h \, \left( T - T_c \right) \text{ on } \Gamma_R^{axis} \\ \end{matrix} \right.\]

With :

* \(T\) : temperature \((K)\)

* \(Q\) : source term \((K)\)

* \(\rho\) : density \((kg/m^3)\)

* \(h\) : convection coefficient \((W \, m^{-2} / K)\)

* \(C_p\) : thermal capacity \((J/K/kg)\)

* \(T_c\) : cooling temperature \((K)\)

And \(\Delta T = \frac{1}{r} \frac{\partial \left( r T \right)}{\partial r} + \frac{\partial T}{\partial z}\)

5. Geometry

The geometry is a torus in cartesian coordinates \((x,y,z)\) or rectangle in axisymmetric coordinates \((r,z)\).

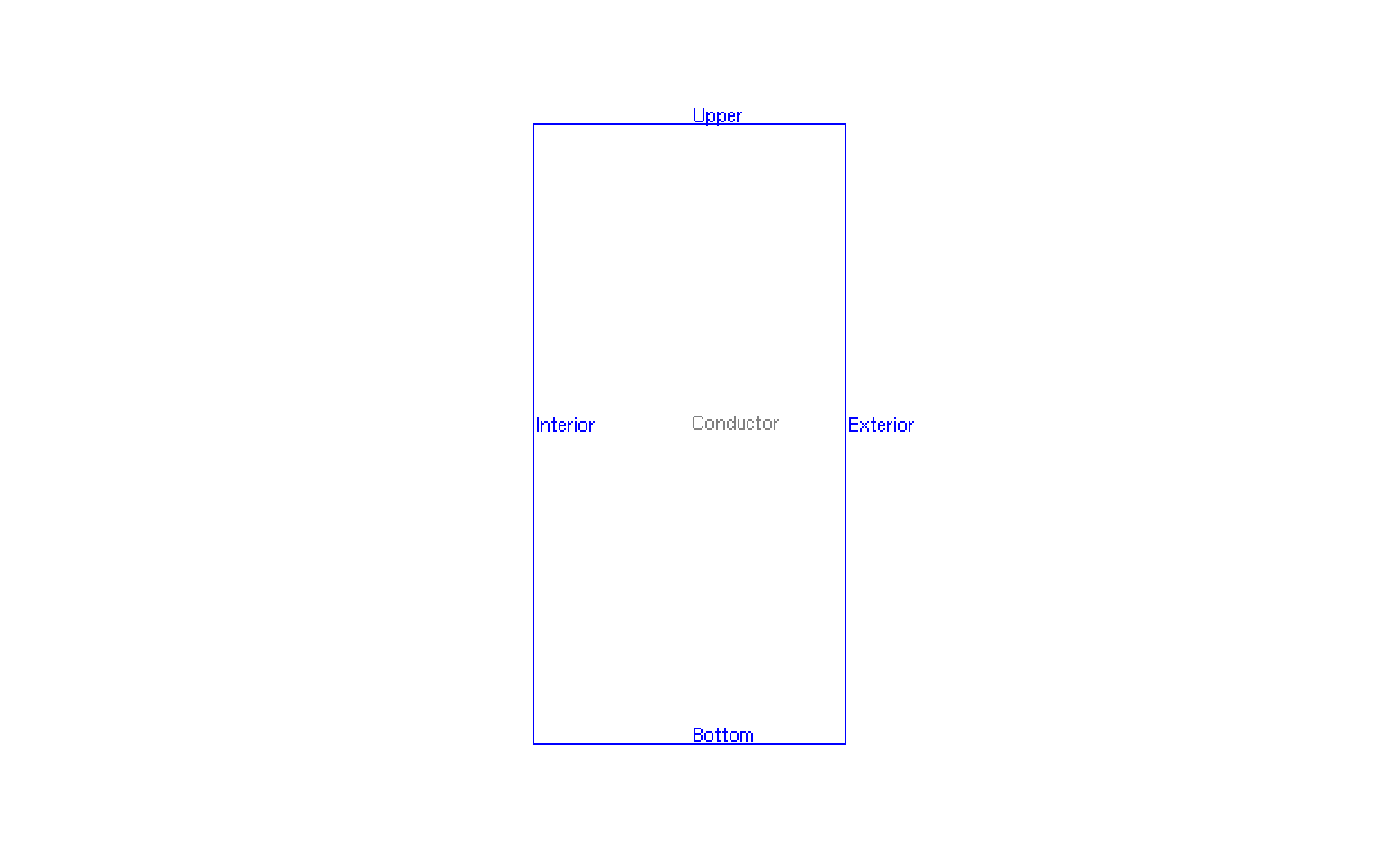
1torus axis
Geometry in Axisymmetrical cut
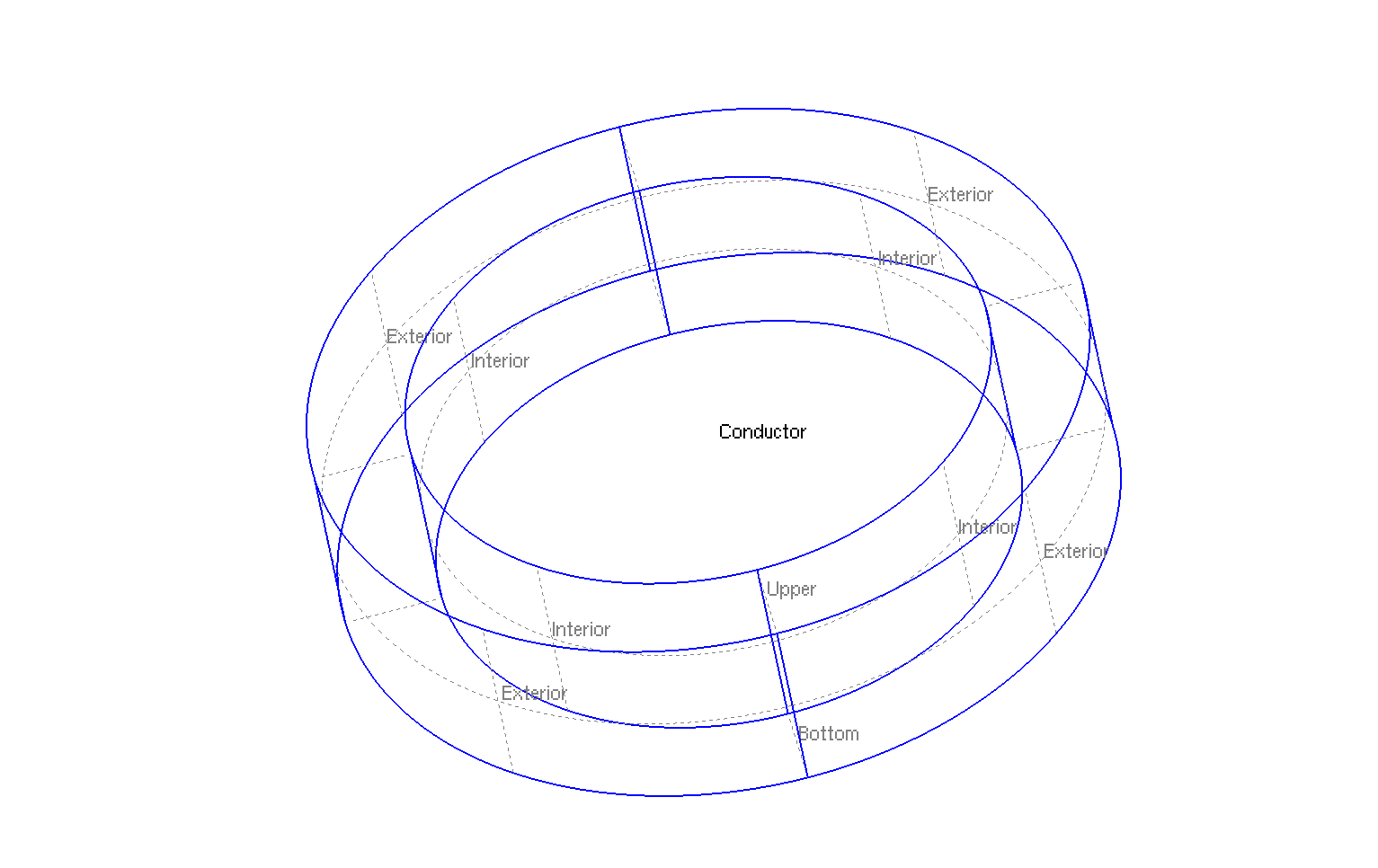
1torus 3d
Geometry in three dimensions

The geometrical domains are :

  • Conductor : the torus, it is composed by the conductive material

  • Interior and Exterior : interior and exterior of ring (or right and left of rectangle in axisymmetric coordinates \((r,z)\)) correspond to \(\Gamma_R\)

  • Bottom and Upper : up and bottom of the ring (or up and bottom of the rectangle in axisymmetric coordinates \((r,z)\)) correspond to \(\Gamma_N\)

Symbol

Description

value

unit

\(r_{int}\)

interior radius of torus

\(75e-3\)

m

\(r_{est}\)

exterior radius of torus

\(100.2e-3\)

m

\(z_1\)

half-height of torus

\(25e-3\)

m

6. Initial/Boundary Conditions

We impose the boundary conditions :

  • Neumann : \(\frac{\partial T}{\partial \mathbf{n}} = 0\) on Interior and Exterior

  • Robin : \(-k \, \frac{\partial T}{\partial \mathbf{n}} = h \, \left( T - T_c \right)\) on Upper and Bottom

We initialize on Conductor, \(T(t=0,r,z) = T_i\)

On JSON file, the boundary conditions are writed :

Boundary conditions on JSON file
    "BoundaryConditions":
    {
        "heat":
        {
            "Robin":
            {
                "Interior":
                {
                    "expr1":"h*x:h:x",
                    "expr2":"h*T_c*x:h:T_c:x"
                },
                "Exterior":
                {
                    "expr1":"h*x:h:x",
                    "expr2":"h*T_c*x:h:T_c:x"
                }
            }
        }
    }

On JSON file, the initial conditions are writed :

Initial conditions on JSON file
    "InitialConditions":
    {
        "temperature":
        {
            "Expression":
            {
                "myic":
                {
                    "markers":"Conductor",
                    "expr":"T_i:T_i"
                }
            }
        }
    }

7. Weak Formulation

We obtain :

Weak Formulation of Heat Equation in axisymmetric coordinates
\[\small{ \text{(Weak Heat Axis)} \int_{\Omega_c^{axis}}{ \rho C_p \, \frac{\partial T}{\partial t} \, \phi \, r \, drdz } + \int_{\Omega_c^{axis}}{ k \, \tilde{\nabla} T \cdot \tilde{\nabla} \phi \, r \, drdz } + \int_{\Gamma_R^{axis}}{ h \, T \, \phi \, r \, d\Gamma } = \int_{\Omega_c^{axis}}{ Q \, \phi \, r \, drdz } + \int_{\Gamma_R^{axis}}{ h \, T_c \, \phi \, r \, d\Gamma } }\]

With \(\tilde{\nabla} = \pmatrix{ \frac{\partial}{\partial r} \\ \frac{\partial}{\partial z} }\)

8. Parameters

The parameters of problem are :

  • On Conductor :

Symbol

Description

Value

Unit

\(Q\)

source term

\(\sigma \, \left( \frac{U}{2\pi \, r} \right)\)

J

\(U\)

electrical potential

\(1\)

\(Volt\)

\(\sigma\)

electrical conductivity

\(58e6\)

\(S/m\)

\(k\)

thermal conductivity

\(380\)

\(W/m/K\)

\(C_p\)

thermal capacity

\(380\)

\(J/K/kg\)

\(\rho\)

density

\(10000\)

\(kg/m^3\)

\(h\)

convective coefficient

\(80000\)

\(W/m^2/K\)

\(T_c\)

cooling temperature

\(293\)

\(K\)

\(T_i\)

initial temperature

\(293\)

\(K\)

On JSON file, the parmeters are writed :

Parameters on JSON file
    "Parameters":
    {
        "h":80000,  // W/m2/K
        "T_c":293,  // K
        "T_i":293,  // K
        "U":1,      // V

        // Constants of analytical solve
        "a":1933.10,    // K
        "b":0.40041,    // K
        "rmax":0.0861910719118454,  // m
        "Tmax":364.446  // K
    }

9. Coefficient Form PDEs

We use the application Coefficient Form PDEs. The coefficient associate to Weak Formulation are :

  • On Conductor :

Coefficient

Description

Expression

\(d\)

damping or mass coefficient

\(\rho \, C_p\)

\(c\)

diffusion coefficient

\(k\)

\(f\)

source term

\(\sigma \left( \frac{U}{2\pi \, r} \right)^2\)

On JSON file, the coeficients are writed :

CFPDEs coefficients on JSON file
    "Materials":
    {
        "Conductor":
        {
            "k":380,        // W/m/K
            "sigma":58e+6,  // S.m-1
            "rho":10000,    // kg/m3
            "Cp":380,       // J/K/kg
            "heat_c":"k*x:k:x",
            "heat_f":"sigma*(U/2/pi)*(U/2/pi)/x:sigma:U:x",
            "heat_d":"rho*Cp*x:rho:Cp:x"
        }
    }

10. Numeric Parameters

  • Size of mesh : \(0.1 \,mm\)

  • Time Parameters :

    • Time step : \(0.5 \, s\)

    • Initial Time : \(0 \, s\)

    • Final Time : \(15 \, s\)

  • Element type : \(P1\)

  • Solver : automatic

  • Number of CPU core : \(16\)

1torus axis mesh
Mesh of Geometry

11. Results

We obtain :

Temperature \(T(K)\)

I plot the maximal temperature \(T_{max}\) across time :

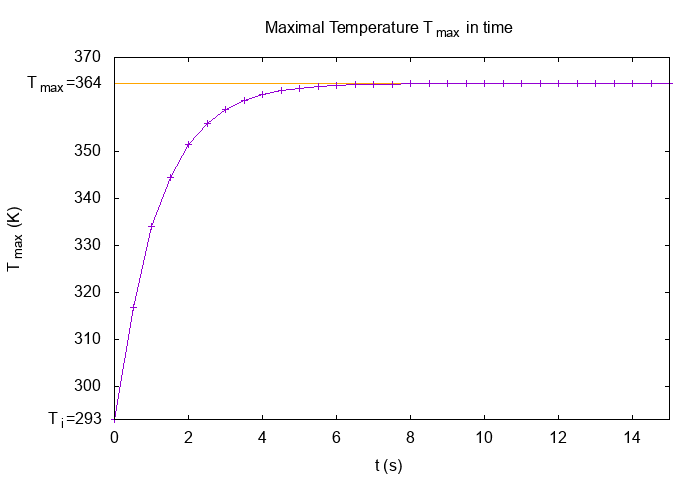
Tmax t
\(T_{max}\) \((K)\) in time

The maximum temperature increase in time and stabilized around \(T_{max}=364 \, K\).

I plot the temperature at \(t=15s\), at this time, we consider the system stationary.

T Or 15s
\(T\) \((K)\) on \(Or\) axis at \(t=15s\)

The temperature is constant by \(z\). We can see with the cut, the temperature have a profil of bell. The temperature is less at the cooled interior and exterior than the middle of torus.

12. Validation

We do a convergence test with L2-error between the numeric result of stationnary problem and stationnary analytical result with different size of mesh.

12.1. Exact solution

The computation are on page Test case of Stationary Heat Equation in Axisymetric.

We have :

\[ T(r) = - a ln^2(\frac{r}{r_{max}}) + T_{max}\]

With \(T_{max} = T(r_{max})\) the maximal temperature and \(r_{max}\) its input.

And :

\[ r_{max} = e^{\frac{T_{c \, int}-T_{c \, ext} + ac}{2 \, a \, b}}\]
\[ T_{max} = \frac{2 \, a \, k}{h_{int} r_{int} + h_{ext} r_{ext}} \, ln(h_{int} r_{int} + h_{ext} r_{ext}) + \frac{h_{int} r_{int} T_{c \, int} + h_{ext} r_{ext} T_{c \, ext}}{h_{int} r_{int} + h_{ext} r_{ext}} + a \frac{ h_{int} r_{int} ln^2(\frac{r_{int}}{r_{max}}) + h_{ext} r_{ext} ln^2(\frac{r_{ext}}{r_{max}}) }{h_{int} r_{int} + h_{ext} r_{ext}}\]

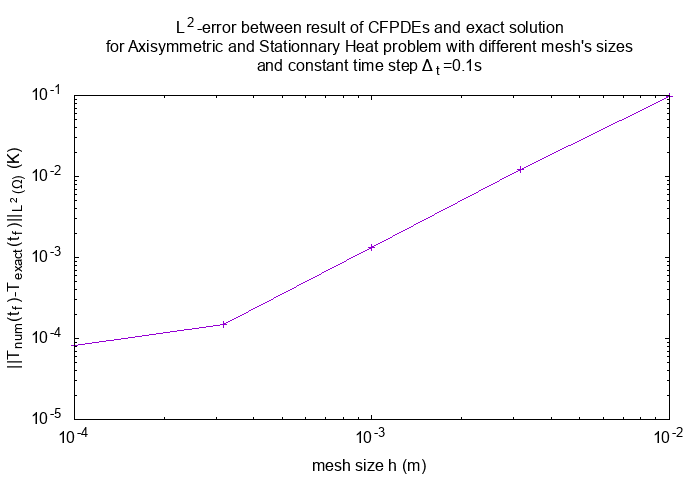
12.2. Convergence Test

I compute the L2-error between the numeric result at final time \(t=t_f\) and exact solution of static problem (\(||T_{num}(t=t_f)-T_{exact}(t=t_f)||_{L^2(\Omega)}\)) for different mesh sizes and a constant time step \(\Delta_t=0.1s\).

convergence h
Table 1. Table of data
hsize (m) \(\Vert T_{num}(t=t_f) - T_{exact}(t=t_f) \Vert_{L^2(\Omega)} (K)\)

0.01

9.596739e-02

0.00316

1.233484e-02

0.001

1.324666e-03

0.000316

1.496172e-04

0.0001

8.224669e-05

Our implementation of transient heat equation in axisymmetrical coordinates converges.