Test Case : getDP - Pancake

1. Introduction

This is the test case of High-Temperature Superconductors with transport current using the T-A Formulation on a Pancake geometry surrounded by air in axisymmetric coordinates.

2. Run the Calculation

The command line to run this case are :

    gmsh -2 -bin pancake.geo
    getdp -m pancake.msh pancake.pro -solve MagDyn -pos MagDyn

3. Data Files

The case data files are available in Github here :

PRO file - Edit the file
GEO file - Edit the file
Data PRO file - Edit the file

As this case also use the library of functions and formulations of life-HTS, the library files are available in Github here.

4. Equation

The T-A Formulation in axysimmetric coordinates is :

T-A Formulation in axisymmetric coordinates

\[\text{(T-A Axis)} \left\{ \begin{matrix} -\frac{1}{\mu}\Delta A_\theta + \frac{1}{\mu r^2}A_\theta &=& \partial_z T_r & \text{on } \Omega^{axis} & \text{(A Axis)} \\ \begin{pmatrix} 0 & 0\\ 0 & -\rho \end{pmatrix}\Delta T_r &=& \frac{\partial(\partial_z A_\theta)}{\partial t} & \text{on } \Omega_c^{axis} & \text{(T Axis)} \end{matrix} \right.\]

With :

\(A_\theta\) : \(\theta\) component of potential magnetic field
\(T_r\) : \(r\) component of potential current density
\(\rho\) : electric resistivity \(\Omega \cdot m\)
\(\mu\) : electric permeability \(kg/A^2/S^2\)

5. Geometry

The geometry is a set of stacked tapes in axisymmetric coordinates \((r,z)\), surrounded by air.

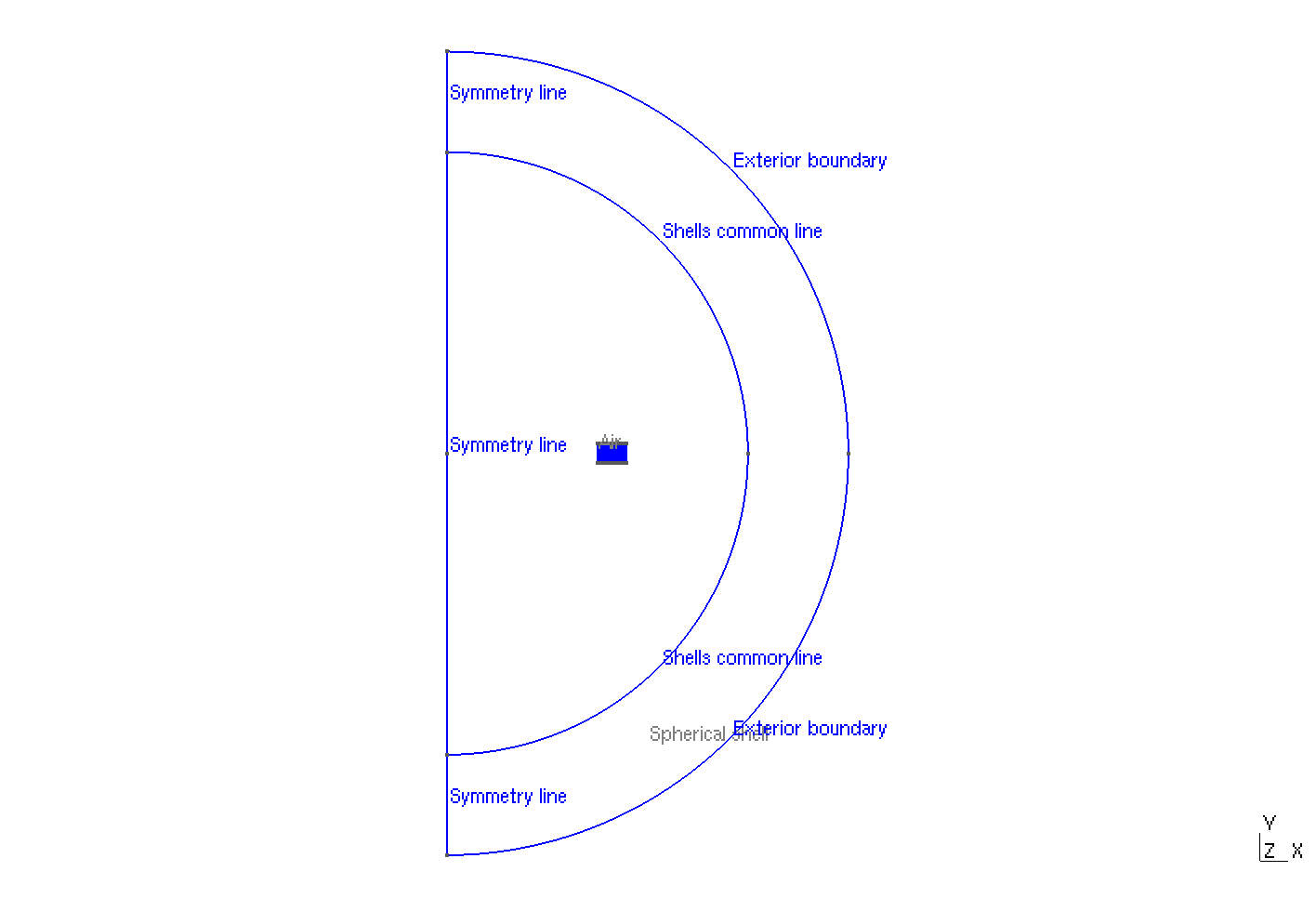
Geometry

Zoom on Tapes

The geometrical domains are :

Conducting domain : the tapes
- Upper Edge : the top boundary of the tapes
- Lower Edge : the bottom boundary of the tapes
- Conducting domain boundary : the side boundaries of the tapes
Air : the air surrounding Conductor
- Symmetry Line : the boundary for the symmetry in axisymmetric coordinates
Spherical Shell : the air surrounding Conductor
- Exterior boundary : the Spherical Shell 's boundary

Symbol

Description

value

unit

\(W_{tapes} (\delta)\)

tapes width

\(1e-6\)

\(H_{tapes}\)

tapes height

\(4e-3\)

\(step\)

space between the tapes

\(0.15e-3\)

\(R_{inf}\)

radius of infty border

\(0.08\)

6. Parameters

The parameters of the problem are :

On Tapes :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

\(Wid\)

tapes width

\(1e-6\)

\(m\)

\(Hei\)

tapes height

\(4e-3\)

\(m\)

\(f\)

frequency

\(50\)

\(Hz\)

\(Imax\)

max current

\(120\)

\(A\)

\(Iapp\)

applied current

\(0.8*Imax*sin(2*\pi*f*t)\)

\(A\)

\(j_c\)

critical current density

\(3.10^{10}\)

\(A/m^2\)

\(e_c\)

threshold electric field

\(10^{-4}\)

\(V/m\)

\(n\)

material dependent exponent

\(40\)

\(\rho\)

electrical resistivity (described by the \(e-j\) power law)

\(\frac{e_c}{j_c}\left(\frac{\mid\mid \partial_z T_r \mid\mid}{j_c}\right)^{(n)}\)

\(\Omega\cdot m\)

On Air :

Symbol

Description

Value

Unit

\(\mu=\mu_0\)

magnetic permeability of vacuum

\(4\pi.10^{-7}\)

\(kg \, m / A^2 / S^2\)

The parameters are separated between the PRO file, the PRO data file, and the files within the folder lib. On PRO file, the parameters are written :

Parameters on PRO file

Function{
    // ------- PARAMETERS -------
    // Superconductor parameters
    DefineConstant [jc = {3e10, Name "Input/3Material Properties/2jc (Am⁻²)"}]; // Critical current density [A/m2]
    DefineConstant [n = {40, Name "Input/3Material Properties/1n (-)"}]; // Superconductor exponent (n) value [-]

    // Excitation
    DefineConstant [IFraction = {0.8, Name "Input/4Source/0Fraction of max. current intensity (-)"}];
    DefineConstant [Imax = IFraction*jc*W_tape*H_tape]; // Maximum imposed current intensity [A]
    DefineConstant [f = 50]; // Frequency of imposed current intensity [Hz]
    DefineConstant [timeStart = 0]; // Initial time [s]
    DefineConstant [timeFinal = 1/f]; // Final time for source definition [s]
    DefineConstant [timeFinalSimu = 1/f]; // Final time of simulation [s]

    // Sine source field
    I[] = Imax * Sin[2.0 * Pi * f* $Time];

    // For the t-a-formulation
    thickness[Cond] = W_tape;
    thickness[Edge2] = W_tape;
    thickness[Air] = W_tape;
}

Parameters on PRO data file

// ---- Geometry parameters ----
DefineConstant[
changeGeometry = {0, Choices{0,1}, Name "Input/1Geometry/1Show geometry?"},
R_inf = {0.08, Visible changeGeometry, Name "Input/1Geometry/Outer radius (m)"}, // Outer shell radius [m]
R_air = {0.06, Max R_inf, Visible changeGeometry, Name "Input/1Geometry/Inner radius (m)"}, // Inner shell radius [m]
H_tape = {4e-3, Max R_air/2, Visible changeGeometry, Name "Input/1Geometry/Tapes height(m)"}, // Width of the tape [m]
W_tape = {1e-6, Max R_air/2, Visible changeGeometry, Name "Input/1Geometry/Tapes Width(m)"}, // Height of the tape [m]
W = {W_tape}, // Width of the tape [m]
sep = {0.15e-3, Visible changeGeometry, Name "Input/1Geometry/separation between tapes(m)"},
meshLayerWidthTape = {0.001} // Width of the control mesh layer around the cylinder
];

The rest of the parameters are defined in the library file lawsAndFunctions.pro

7. Boundary Conditions

For the Dirichlet boundary conditions, we want to impose the transport current :

The transport current is the difference of current potential between the top and the bottom of the tapes divided by the thickness of the tapes, so we can impose \(0\) at the bottom and \(Iapp/thickness\) at the top of the tapes.

Finally we have :

On Top : \(T_r = Iapp/\delta\)
On Bottom : \(T_r = 0\)

On PRO file, the boundary conditions are written :

Boundary conditions on EDP file

Constraint {
    { Name Current ; Type Assign;
        Case {
            // t-a-formulation
            { Region Edge2; Value 1.0; TimeFunction I[]; }
        }
    }
}

8. Weak Formulation

Weak formulation of T-A Formulation in axisymmetric coordinates

\[\scriptsize{ \text{(Weak TA Axis)} \left\{ \begin{eqnarray*} \int_{\Omega^{axis}}{ \frac{r}{\mu} \tilde\nabla A_\theta \cdot \tilde\nabla \phi \ drdz } + \int_{\Omega^{axis}}{\frac{1}{\mu r} A_\theta \cdot \phi \ drdz} = \int_{\Omega^{axis}_c}{ \frac{\partial T_r}{\partial z} \cdot\phi \ rdrdz } \\ \int_{\Omega^{axis}_c}{ \begin{pmatrix} 0 & 0 \\ 0 & \rho \end{pmatrix} \tilde\nabla T_r \cdot \tilde\nabla \varphi \ drdz } = \int_{\Omega^{axis}_c}{ \frac{\partial (\partial_z A_\theta}{\partial t} \cdot\varphi \ rdrdz }\\ \text{for } \phi \in H^1(\Omega) \text{ and } \varphi \in H^1(\Omega_c) \end{eqnarray*} \right. }\]

9. Implementation of the Weak Formulation

On getDP, we need to implement the Weak Formulation.

The T-A formulation is implemented in the library file formulations.pro :

On MPH file, the coefficients are written :

T-A formulation on formulations.pro

{ Name MagDyn_ta; Type FemEquation;
        Quantity {
            { Name t; Type Local; NameOfSpace t_space; }
            { Name T; Type Global; NameOfSpace t_space[T]; }
            { Name V; Type Global; NameOfSpace t_space[V]; }
            { Name a; Type Local; NameOfSpace a_space_2D; }
        }
        Equation {
            // Time derivative - current solution
            Galerkin { [ - Normal[] /\ Dof{a} , {d t} ];
                In OmegaC; Integration Int; Jacobian Sur;  }
            // Time derivative - previous solution
            Galerkin { [ Normal[] /\ {a}[1] , {d t} ];
                In OmegaC; Integration Int; Jacobian Sur;  }
            // ---- SUPER ----
            // Induced currents
            // Non-linear OmegaC
            Galerkin { [ - $DTime * 1./thickness[] * rho[1./thickness[] *{d t} /\ Normal[], 1./thickness[] *mu[]*Norm[{t}] ] * Normal[] /\ (Dof{d t} /\ Normal[]) , {d t} ];
                    In NonLinOmegaC; Integration Int; Jacobian Sur;  }
            GlobalTerm { [ - $DTime * Dof{V} , {T} ] ; In PositiveEdges ; }
            // Surface term
            Galerkin { [ - Dof{d t} /\ Normal[] , {a}];
                In BndOmega_ha; Integration Int; Jacobian Sur; }
        }
    }

10. Numeric Parameters

Time
- Initial Time : \(0s\)
- Final Time : \(0.02s\)
- Time Step : \(2e-4s\)
Mesh

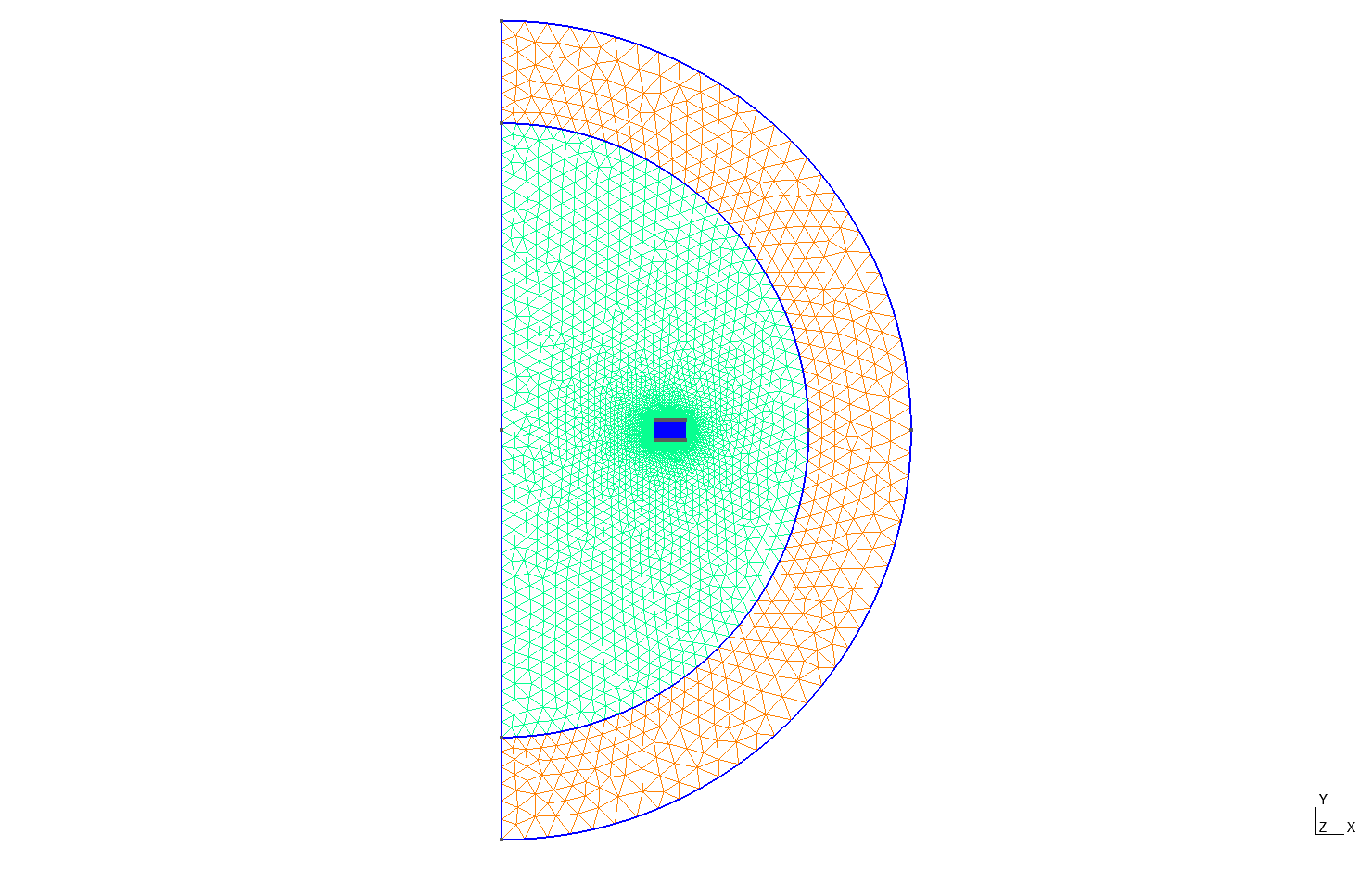
Mesh

11. Results

The results that we obtain with the T-A formulation with getDP are compared to the results of the article COMSOL implementation of the H-φ-formulation with thin cuts for modeling superconductors with transport currents where the solver Comsol is used with the H-φ Formulation.

11.1. Electric current density

The electric current density \(J\) is defined by :

\[ J_\theta = \frac{\partial T}{\partial z}\]

Electric current density \(J_\theta (A/m^2)\)

We compare the current density profiles with the T-A formulation on getDP and the H-φ formulation on Comsol on the \(O_z\) axis, on the middle tape of the pancake, at time \(t=0.02s\) for a maximum applied current of 150 T and \(n=40\).

11.2. Magnetic flux density

The magnetic flux density \(B\) is defined by:

\[ B=\nabla\times A =\begin{pmatrix}-\partial_z A_\theta\\ 0\\ \frac{1}{r}\partial_r (rA_\theta)\end{pmatrix}\]

Magnitude of the magnetic flux density \(B (T)\)

We can see that when the transport current is applied the tapes are generating a magnetic field, that stay trapped in the superconductor once the applied current is 0.

We compare the distribution of the r-component of the magnetic flux density with the T-A formulation on getDP and the H-φ formulation on Comsol on the \(Oz\) axis, in the middle of the pancake \(t=0.02s\).

L2 Relative Error Norm : \(3.75 \%\)

12. References

Real-time simulation of large-scale HTS systems: multi-scale and homogeneous models using the T–A formulation, Edgar Berrospe-Juarez et al 2019 Supercond. Sci. Technol. 32 065003, PDF

COMSOL Implementation of the H-ϕ-Formulation With Thin Cuts for Modeling Superconductors With Transport Currents, A. Arsenault, B. d. S. Alves and F. Sirois, in IEEE Transactions on Applied Superconductivity, vol. 31, no. 6, pp. 1-9, Sept. 2021, Art no. 6900109, doi: 10.1109/TASC.2021.3097245. PDF