Test Case of Magnetostatic
1. Introduction
This is the test case of Maxwell Quasi Static Problem with the A-V Formulation and Gauge Condition on a torus geometry surrounded by air for the stationnary case in axisymmetric coordinates.
2. Run the Calculation
The command line to run this case is :
mpirun -np 16 feelpp_toolbox_coefficientformpdes --config-file=magnetostatic.cfg --cfpdes.gmsh.hsize=1e-3
This case is run with the latest version 109 of Feelpp.
3. Data Files
The case data files are available in Github here :
-
CFG file - Edit the file
-
JSON file - Edit the file
-
GEO file - Edit the file
4. Equation
Assuming that \(V\) is known, the A-V Formulation in axisymmetric coordinates (MagnetoStatic Axis) for the stationary case is :
With :
-
\(A_{\theta}\) : \(\theta\) component of potential magnetic field
-
\(\sigma\) : electric conductivity \(S/m\)
-
\(\mu\) : electric permeability \(kg/A^2/S^2\)
-
\(U\) : tension \(Volt\)
5. Geometry
The geometry is a rectangle in axisymmetric coordinates \((r,z)\) representing a conducting torus, surrounded by air.
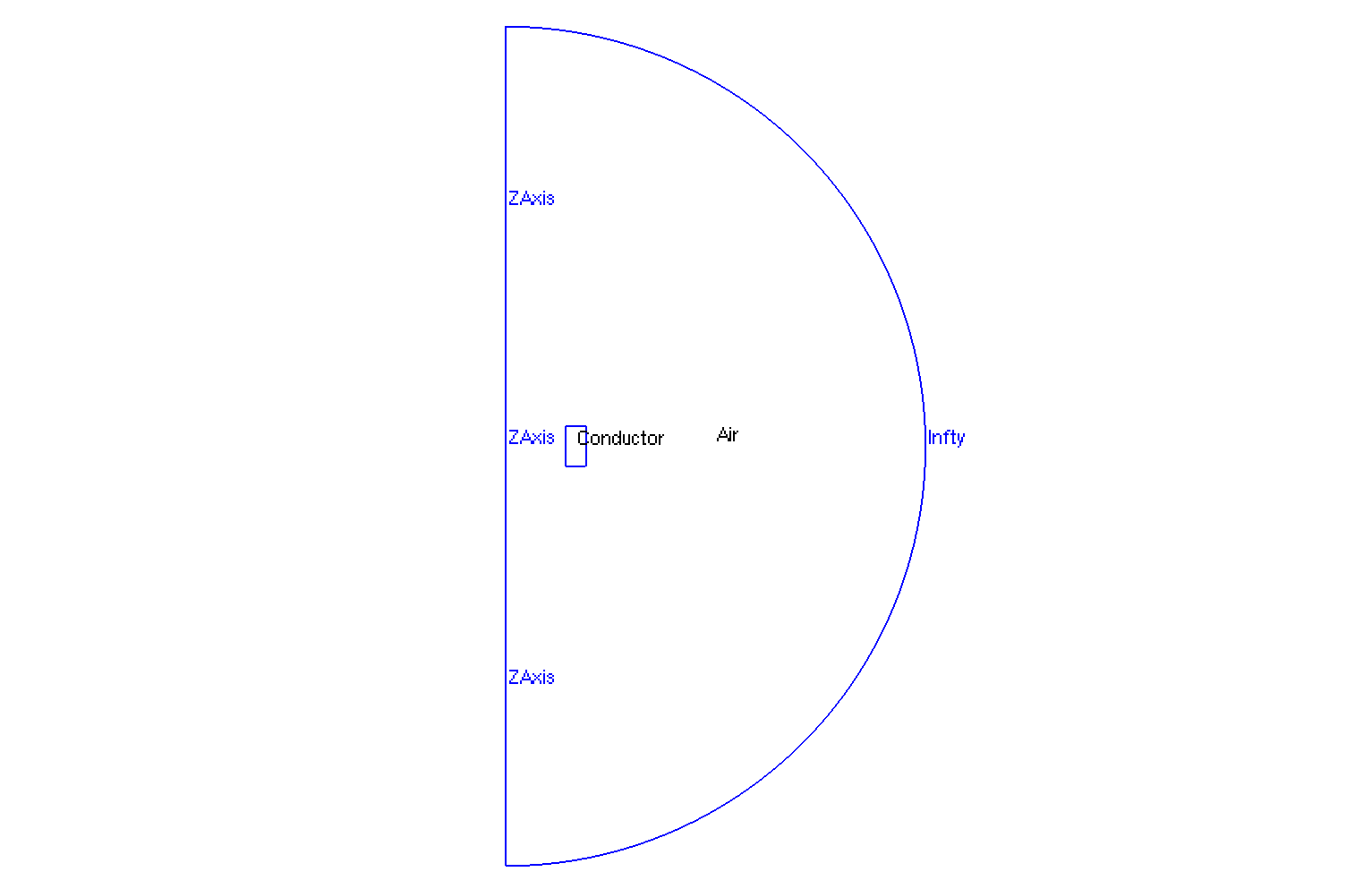
Geometry in Axisymmetrical cut
|
The geometrical domains are :
-
Conductor: the torus, composed by a conductor -
Air: the air surroundingConductor-
zAxis:Air's bound, correspond to \(Oz\) axis (\(\{(z,r), \, z=0 \}\)) -
infty: the rest of theAir's bound
-
Symbol |
Description |
value |
unit |
\(r_{int}\) |
interior radius of torus |
\(75e-3\) |
m |
\(r_{ext}\) |
exterior radius of torus |
\(100.2e-3\) |
m |
\(z_1\) |
half-height of torus |
\(25e-3\) |
m |
\(r_{infty}\) |
radius of infty border |
\(5*r_{ext}\) |
m |
6. Boundary Conditions
The Dirichlet boundary conditions imposed are :
-
On
zAxis: \(A_{\theta} = 0\) -
On
infty: \(A_{\theta} = 0\)
On JSON file, the boundary conditions are written :
"BoundaryConditions":
{
"magnetic":
{
"Dirichlet":
{
"ZAxis":
{
"expr":"0"
},
"Infty":
{
"expr":"0"
}
}
}
}
7. Weak Formulation
With \(\tilde{\nabla} = \begin{pmatrix} \partial r \\ \partial z \end{pmatrix}\)
8. Parameters
The parameters of the problem are :
-
On
Conductor:
Symbol |
Description |
Value |
Unit |
\(V\) |
scalar electrical potential |
\( U \, \frac{\theta}{2\pi}\) |
\(Volt\) |
\(U\) |
electrical potential |
\(1\) |
\(Volt / rad\) |
\(\sigma\) |
electrical conductivity |
\(58e6\) |
\(S/m\) |
\(\mu=\mu_0\) |
magnetic permeability of vacuum |
\(4\pi.10^{-7}\) |
\(kg \, m / A^2 / S^2\) |
-
On
Air:
Symbol |
Description |
Value |
Unit |
\(\mu=\mu_0\) |
magnetic permeability of vacuum |
\(4\pi.10^{-7}\) |
\(kg \, m / A^2 / S^2\) |
On JSON file, the parameters are written :
"Parameters":
{
"U":"1" // Volt
}
9. Coefficient Form PDEs
The Feelpp toolboxe Coefficient Form PDEs is used here. The coefficients associated to the Weak Formulation are :
-
On
Conductor:
Coefficient |
Description |
Expression |
\(c\) |
diffusion coefficient |
\(\frac{r}{\mu}\) |
\(a\) |
absorption or reaction coefficient |
\(\frac{1}{\mu r}\) |
\(f\) |
source term |
\(- \sigma \frac{U}{2\pi}\) |
-
On
Air:
Coefficient |
Description |
Expression |
\(c\) |
diffusion coefficient |
\(\frac{r}{\mu}\) |
\(a\) |
absorption or reaction coefficient |
\(\frac{1}{\mu r}\) |
On JSON file, the coefficients are written :
"Materials":
{
"Conductor":
{
"magnetic_c":"x/mu:x:mu",
"magnetic_a":"1/mu/x:mu:x",
"magnetic_f":"-sigma*U/2/pi:sigma:U"
},
"Air":
{
"magnetic_c":"x/mu:x:mu",
"magnetic_a":"1/mu/x:mu:x"
}
}
10. Numeric Parameters
-
Mesh size :
-
Interior of torus : \(0.001 m\)
-
Far from torus : \(0.004 m\)
-
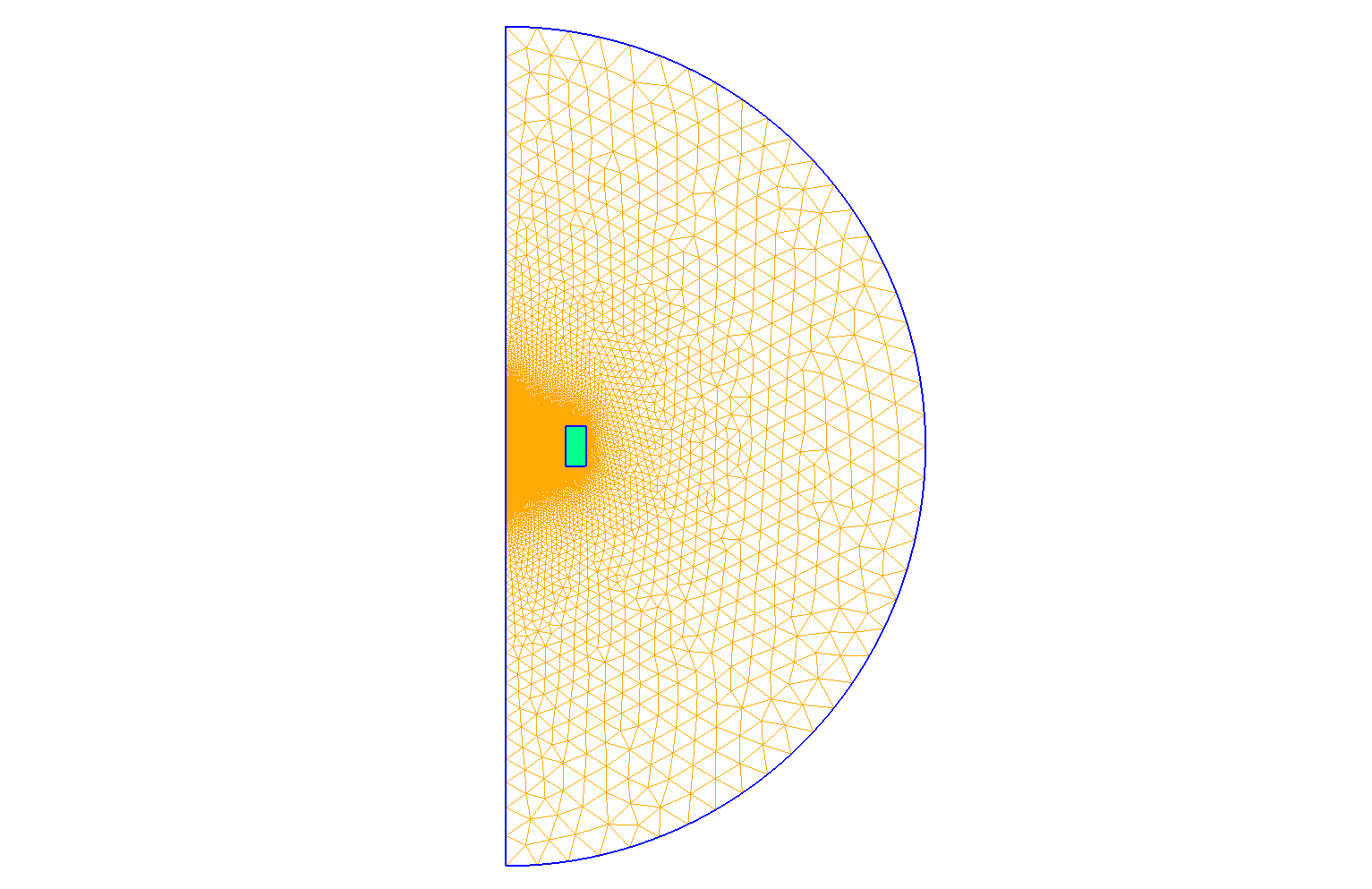
Mesh of Geometry
|
11. Results
11.1. Magnetic Potential Field
The magnetic potential field \(\mathbf{A}\) defined by :
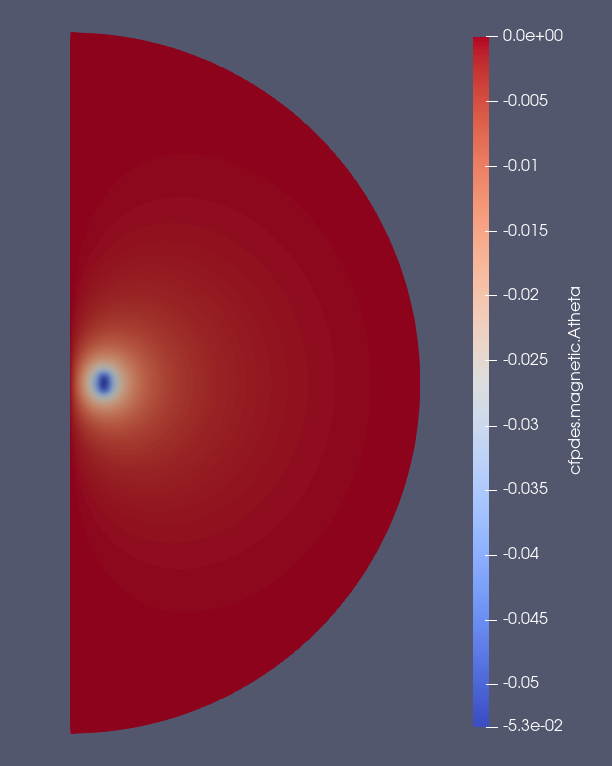
\(A_{\theta} (A.m)\)
|
The behavior of \(A_\theta\) on the \(O_r\) axis is as follows :
h |
L2 Error Norm |
L2 Relative Error Norm |
\(9e-3\) |
\(8.71956e-3\) |
\(2.04\%\) |
\(5e-3\) |
\(7.93963e-3\) |
\(1.87\%\) |
\(1e-3\) |
\(7.64198e-3\) |
\(1.80\%\) |
\(5e-4\) |
\(7.63809e-3\) |
\(1.80\%\) |
11.2. Magnetic Field
The magnetic field \(\mathbf{B}\) is defined by :
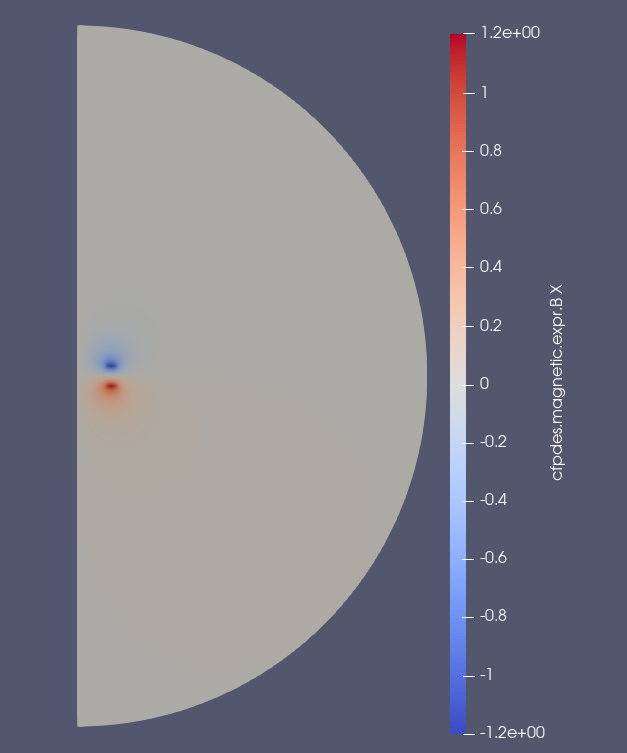
\(B_r (T)\)
|
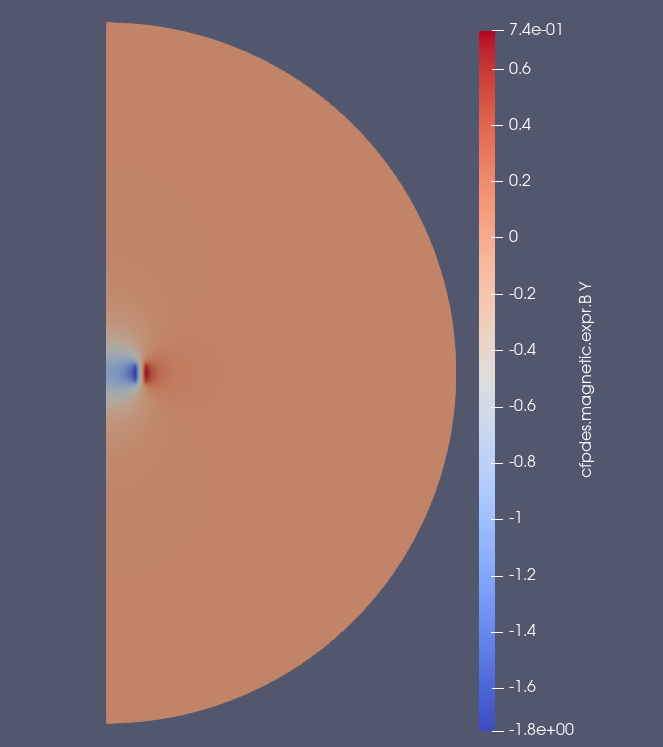
\(B_z (T)\)
|
The behavior of \(\mathbf{B}_z\) on the \(O_z\) axis :
h |
L2 Error Norm |
L2 Relative Error Norm |
\(9e-3\) |
\(15.462408e-2\) |
\(2.12\%\) |
\(5e-3\) |
\(7.717275e-2\) |
\(1.06\%\) |
\(1e-3\) |
\(3.074955e-2\) |
\(0.42\%\) |
\(5e-4\) |
\(2.982289e-2\) |
\(0.41\%\) |